
若函數 ,則對于不同的實數a,函數
,則對于不同的實數a,函數 的單調區間個數不可能是( )
的單調區間個數不可能是( )
| A.1個 | B.2個 | C.3個 | D.5個 |
B
解析試題分析:最高次項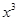 遞增,無論a如何取值,當x---> +∞時,f(x)遞增;
遞增,無論a如何取值,當x---> +∞時,f(x)遞增;
當x從左邊-∞開始(當然沒有開始)時, f(x)遞增。
由于曲線是連續的,所以,(1)若中間連續遞增,(a=0時)單調區間個數為1;
(2) 若中間只有一段遞減,即增,減,增單調區間個數為3;
(3)若中間有2段遞減,即增,減,增,減,增單調區間個數為5;
總之單調區間個數不可能為2。
另,無論x取何值,a取何值,原函數被分成三部分討論(-∞,-1),[-1,1],(1,+∞).當a=0時,是一個單調區間,a不等于零時,三次函數,則不可能有兩個單調區間 ,故選B 。
考點:函數的圖象,應用導數研究函數的單調性。
點評:中檔題,作為選擇題,在解答過程中,可借助于就的函數的單調性,做出定性分析,簡化解答過程。本題為選擇題,不必“小題大作”。


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com