
定義在R上的函數 ,對任意不等的實數
,對任意不等的實數 都有
都有 成立,又函數
成立,又函數 的圖象關于點(1,0)對稱,若不等式
的圖象關于點(1,0)對稱,若不等式 成立,則當1≤x<4時,
成立,則當1≤x<4時, 的取值范圍是
的取值范圍是
A. | B. | C. | D. |
A
解析試題分析:解:因為對任意不等實數x1,x2滿足 所以函數f(x)是定義在R上的單調遞減函數.因為函數y=f(x-1)的圖象關于點(1,0)對稱,所以函數y=f(x)的圖象關于點(0,0)對稱,即函數f(x)是定義在R上的奇函數.又因為對于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立,所以f(x2-2x)≥f(-2y+y2)成立,所以根據函數的單調性可得:對于任意的x,y∈R,不等式x2-2x≥y2-2y成立,即(x-y)(x+y-2)≥0(1≤x≤4),所以可得其可行域,如圖所示:
所以函數f(x)是定義在R上的單調遞減函數.因為函數y=f(x-1)的圖象關于點(1,0)對稱,所以函數y=f(x)的圖象關于點(0,0)對稱,即函數f(x)是定義在R上的奇函數.又因為對于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立,所以f(x2-2x)≥f(-2y+y2)成立,所以根據函數的單調性可得:對于任意的x,y∈R,不等式x2-2x≥y2-2y成立,即(x-y)(x+y-2)≥0(1≤x≤4),所以可得其可行域,如圖所示: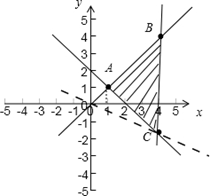
因為 =
= 所以
所以 表示點(x,y)與點(0,0)連線的斜率,所以結合圖象可得:
表示點(x,y)與點(0,0)連線的斜率,所以結合圖象可得: 的最小值是直線OC的斜率-
的最小值是直線OC的斜率- ,最大值是直線AB的斜率1,所以
,最大值是直線AB的斜率1,所以 的范圍為:[
的范圍為:[ 故答案為:
故答案為:
考點:抽象函數的性質
點評:解決此類問題的關鍵是熟練掌握抽象函數的性質的證明與判斷,如單調性、奇偶性的證明與判斷,并且熟練的利用函數的性質解有關的不等式,以及熟練掌握線性規劃問題,此題綜合性較強知識點也比較零散,對學生掌握知識與運用知識的能力有一定的要求.


 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:高中數學 來源: 題型:單選題
根據表格中的數據,可以判定函數 的一個零點所在的區
的一個零點所在的區 ,則
,則 的值為( )
的值為( )
 | -1 | 0 | 1 | 2 | 3 |
 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
 | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知函數 的圖象是連續不斷的,且有如下對應值表:
的圖象是連續不斷的,且有如下對應值表:
 | 1 | 2 | 3 | 4 | 5 |
 |  |  | 1 | 4 | 7 |
 必有零點的區間為( ).
必有零點的區間為( ).查看答案和解析>>
科目:高中數學 來源: 題型:單選題
國際上鉆石的重量計量單位是克拉,已知某種鉆石的價值V(美元)與其重量W(克拉)之間的函數關系為 ,若把一顆鉆石切割成1︰3的兩顆鉆石,則價值損失的百分率為( )(價值損失百分率
,若把一顆鉆石切割成1︰3的兩顆鉆石,則價值損失的百分率為( )(價值損失百分率 ,切割中重量損耗不計)
,切割中重量損耗不計)
| A.12.5% | B.37.5% | C.50% | D.62.5% |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com