
【題目】如圖,已知![]() 是直角梯形,且
是直角梯形,且![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.
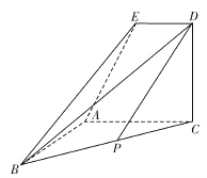
(1)求證:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的左、右頂點分別為A,B,左焦點為F,O為原點,點P為橢圓C上不同于A、B的任一點,若直線PA與PB的斜率之積為
)的左、右頂點分別為A,B,左焦點為F,O為原點,點P為橢圓C上不同于A、B的任一點,若直線PA與PB的斜率之積為![]() ,且橢圓C經過點
,且橢圓C經過點![]() .
.
(1)求橢圓C的方程;
(2)若P點不在坐標軸上,直線PA,PB交y軸于M,N兩點,若直線OT與過點M,N的圓G相切.切點為T,問切線長![]() 是否為定值,若是,求出定值,若不是,請說明理由.
是否為定值,若是,求出定值,若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖a是某市參加2012年高考的學生身高條形統計圖,從左到右的各條形表示的學生人數依次記為![]() 、
、![]() 、…、
、…、![]() [如
[如![]() 表示身高(單位:cm)在
表示身高(單位:cm)在![]() 內的學生人數].圖b是統計圖a中身高在一定范圍內學生人數的一個算法流程圖.現要統計身高在
內的學生人數].圖b是統計圖a中身高在一定范圍內學生人數的一個算法流程圖.現要統計身高在![]() (含160cm,不含180cm)的學生人數,那么在流程圖中的判斷框內應填寫的條件是( )
(含160cm,不含180cm)的學生人數,那么在流程圖中的判斷框內應填寫的條件是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司有一款保險產品的歷史收益率(收益率![]() 利潤
利潤![]() 保費收入)的頻率分布直方圖如圖所示:
保費收入)的頻率分布直方圖如圖所示:
(1)試估計這款保險產品的收益率的平均值;
(2)設每份保單的保費在20元的基礎上每增加![]() 元,對應的銷量為
元,對應的銷量為![]() (萬份).從歷史銷售記錄中抽樣得到如下5組
(萬份).從歷史銷售記錄中抽樣得到如下5組![]() 與
與![]() 的對應數據:
的對應數據:
| 25 | 30 | 38 | 45 | 52 |
銷量為 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 與
與![]() 有較強的線性相關關系,且據此計算出的回歸方程為
有較強的線性相關關系,且據此計算出的回歸方程為![]() .
.

(ⅰ)求參數![]() 的值;
的值;
(ⅱ)若把回歸方程![]() 當作
當作![]() 與
與![]() 的線性關系,用(1)中求出的收益率的平均值作為此產品的收益率,試問每份保單的保費定為多少元時此產品可獲得最大利潤,并求出最大利潤.注:保險產品的保費收入
的線性關系,用(1)中求出的收益率的平均值作為此產品的收益率,試問每份保單的保費定為多少元時此產品可獲得最大利潤,并求出最大利潤.注:保險產品的保費收入![]() 每份保單的保費
每份保單的保費![]() 銷量.
銷量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,點
,點![]() 為動點,以
為動點,以![]() 為直徑的圓內切于
為直徑的圓內切于![]() .
.
(1)證明![]() 為定值,并求點
為定值,并求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 過點
過點![]() 且與
且與![]() 垂直,
垂直,![]() 與
與![]() 交于
交于![]() 兩點,
兩點,![]() 為
為![]() 的中點,求
的中點,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com