
已知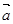 =(
=(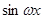 ,
,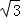
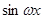 ),
), =(
=(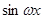 ,
,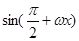 ),(ω>0),
),(ω>0),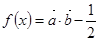 且
且 的最小正周期是
的最小正周期是 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若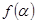 =
=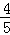 (
(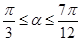 ),求
),求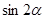 值;
值;
(Ⅲ)若函數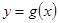 與
與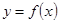 的圖象關于直線
的圖象關于直線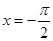 對稱,且方程
對稱,且方程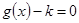 在區間
在區間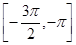 上有解,求
上有解,求 的取值范圍.
的取值范圍.
(1) ;(2)
;(2)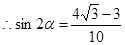 ;(3)
;(3)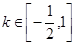 .
.
解析試題分析:1)先用數量積的概念轉化為三角函數的形式,尋求角與角之間的關系,化非特殊角為特殊角;正確靈活運用公式,通過三角變換消去或約去一些非特殊角的三角函數值,注意題中角的范圍;(2)掌握一些常規技巧:“1”的代換,和積互化等,異名三角函數化為同名三角函數,異角化為同角,異次化為同次,切化弦,特殊角與特殊角的三角函數互化;(3)注意利用轉化的思想,本題轉化為求最值,熟悉公式的整體結構,體會公式間的聯系,倍角公式和輔助角公式應用是重點.
試題解析:解:(1)由題意可得
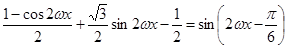 且
且 的周期為
的周期為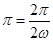 ,求得
,求得 .
.
Ⅱ)由(Ⅰ)得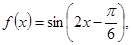 根據
根據
 ,
,
可得 ,
,

(Ⅲ)由于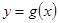 與
與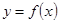 的圖像關于直線
的圖像關于直線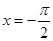 對稱,
對稱,
區間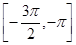 關于直線
關于直線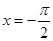 的對稱區間
的對稱區間 ,
,
故本題即求函數
 上的取值范圍,
上的取值范圍,
令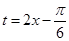 ,
,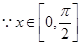 ,可得
,可得 ,
,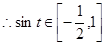 ,
,
即 的范圍為
的范圍為
考點:(1)三角函數的變換;(2)三角函數求值域.


科目:高中數學 來源: 題型:解答題
已知向量a=(cosθ,sinθ),θ∈[0,π],向量b=(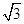 ,-1).
,-1).
(1)若a⊥b,求θ的值;
(2)若|2a-b|<m恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)本題共有2個小題,第1小題滿分4分,第2個小題滿分8分。
已知復數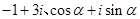 (
(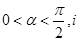 是虛數單位)在復平面上對應的點依次為
是虛數單位)在復平面上對應的點依次為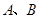 ,點
,點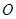 是坐標原點.
是坐標原點.
(1)若 ,求
,求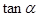 的值;
的值;
(2)若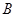 點的橫坐標為
點的橫坐標為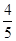 ,求
,求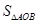 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
平面內動點P到點F(1,0)的距離等于它到直線x=-1的距離,記點P的軌跡為曲線Γ.
(1)求曲線Γ的方程;
(2)若點A,B,C是Γ上的不同三點,且滿足 +
+ +
+ =0,證明:△ABC不可能為直角三角形.
=0,證明:△ABC不可能為直角三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com