
【題目】在直角坐標系xOy中,直線l過點![]() 且傾斜角為
且傾斜角為![]() .以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,已知曲線C的極坐標方程為
.以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,已知曲線C的極坐標方程為![]() ,l與C交于M,N兩點.
,l與C交于M,N兩點.
(1)求C的直角坐標方程和![]() 的取值范圍;
的取值范圍;
(2)求MN中點H的軌跡的參數方程.
【答案】(1)![]() ;
;![]() 或
或![]() (2)
(2)![]() (
(![]() 為參數,且
為參數,且![]() 或
或![]() ).
).
【解析】
(1)直接利用轉換關系的應用,把參數方程極坐標方程和直角坐標方程之間進行轉換.
(2)利用直線的垂直的充要條件的應用求出結果.
解:(1)C的直角坐標方程為![]() ,
,
即![]() ,是以原點為圓心的單位圓
,是以原點為圓心的單位圓
當![]() 時,顯然直線l與曲線C相離,不合題意.
時,顯然直線l與曲線C相離,不合題意.
∴![]() ,所以直線l的斜率
,所以直線l的斜率![]() 存在.
存在.
∴直線l的方程可寫為![]()
∵直線l與曲線C交于M,N兩點,
∴圓心O到直線l的距離![]() ,
,
解得![]()
∴![]() 或
或![]() .
.
(2)(法一)直線l的參數方程為![]()
(t為參數,![]() 或
或![]() )
)
設M,N,H對應的參數分別為![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,
將直線l的參數方程代入曲線C的直角坐標方程得:
![]()
∴![]() ,∴
,∴![]() ,
,
又點H的坐標滿足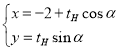 ,
,
(t為參數,![]() 或
或![]() )
)
∴點H的軌跡的參數方程為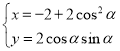
即![]() (
(![]() 為參數,
為參數,![]() 或
或![]() )
)
(法二)
設點![]() ,則由
,則由![]() 可知,
可知,
當![]() 時有
時有![]()
即![]() ,整理得
,整理得![]()
當![]() 時,點H與原點重合,也滿足上式.
時,點H與原點重合,也滿足上式.
∴點H的軌跡的參數方程為![]()
(![]() 為參數,且
為參數,且![]() 或
或![]() ).
).


科目:高中數學 來源: 題型:
【題目】已知函數![]() 和函數
和函數![]() ,關于這兩個函數圖像的交點個數,下列四個結論:①當
,關于這兩個函數圖像的交點個數,下列四個結論:①當![]() 時,兩個函數圖像沒有交點;②當
時,兩個函數圖像沒有交點;②當![]() 時,兩個函數圖像恰有三個交點;③當
時,兩個函數圖像恰有三個交點;③當![]() 時,兩個函數圖像恰有兩個交點;④當
時,兩個函數圖像恰有兩個交點;④當![]() 時,兩個函數圖像恰有四個交點.正確結論的個數為( )
時,兩個函數圖像恰有四個交點.正確結論的個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱錐![]() 中,底面
中,底面![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() ,
,![]() 底面
底面![]() ,點
,點![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.
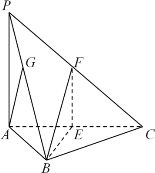
(1)求證:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成的角的余弦值為
所成的角的余弦值為![]() ?若存在,確定點
?若存在,確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】實現國家富強.民族復興.人民幸福是“中國夢”的本質內涵.某商家計劃以“全民健身促健康,同心共筑中國夢”為主題舉辦一次有獎消費活動,此商家先把某品牌乒乓球重新包裝,包裝時在每個乒乓球上印上“中”“國”“夢”三個字樣中的一個,之后隨機裝盒(1盒4個球),并規定:若顧客購買的一盒球印的是同一個字,則此顧客獲得一等獎;若顧客購買的一盒球集齊了“中”“國”二字且僅有此二字,則此顧客獲得二等獎;若顧客購買的一盒球集齊了“中”“國”“夢”三個字,則此顧客獲得三等獎,其它情況不設獎,則顧客購買一盒乒乓球獲獎的概率是_____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系![]() 的原點為極點,
的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位,已知直線
軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位,已知直線![]() 的參數方程為
的參數方程為 ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]()
![]() 求直線
求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
![]() 若把曲線
若把曲線![]() 上給點的橫坐標伸長為原來的
上給點的橫坐標伸長為原來的![]() 倍,縱坐標伸長為原來的
倍,縱坐標伸長為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,設點
,設點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家政公司對部分員工的服務進行民意調查,調查按各項服務標準進行量化評分,嬰幼兒保姆部對40~50歲和20~30歲各20名女保姆的調查結果如下:
分數 年齡 |
|
|
|
|
|
40~50歲 | 0 | 2 | 4 | 7 | 7 |
20~30歲 | 3 | 5 | 5 | 5 | 2 |
(1)若規定評分不低于80分為優秀保姆,試分別估計這兩個年齡段保姆的優秀率;
(2)按照大于或等于80分為優秀保姆,80分以下為非優秀保姆統計.作出![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為對保姆工作質量的評價是否優秀與年齡有關.
的把握認為對保姆工作質量的評價是否優秀與年齡有關.
(3)從所有成績在70分以上的人中按年齡利用分層抽樣抽取10名保姆,再從這10人中選取3人給大家作經驗報告,設抽到40~50歲的保姆的人數為![]() ,求出
,求出![]() 的分布列與期望值.
的分布列與期望值.
下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式: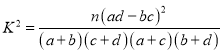 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界第一產糧大國,我國糧食產量很高,整體很安全按照14億人口計算,中國人均糧食產量約為950斤﹣比全球人均糧食產量高了約250斤.如圖是中國國家統計局網站中2010﹣2019年,我國糧食產量(千萬噸)與年末總人口(千萬人)的條形圖,根據如圖可知在2010﹣2019年中( )
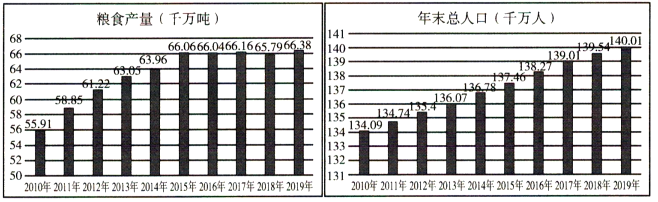
A.我國糧食年產量與年末總人口均逐年遞增
B.2011年我國糧食年產量的年增長率最大
C.2015年﹣2019年我國糧食年產量相對穩定
D.2015年我國人均糧食年產量達到了最高峰
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,極點為![]() ,一條封閉的曲線
,一條封閉的曲線![]() 由四段曲線組成:
由四段曲線組成:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求該封閉曲線所圍成的圖形面積;
(2)若直線![]() :
:![]() 與曲線
與曲線![]() 恰有3個公共點,求
恰有3個公共點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com