分析:(1)依題意點P
n的坐標為(x
n,y
n-1),從而得到
yn+1=4xn+n=
4xn+1,x
n+1=x
n+n,由此能求出數列{x
n}的通項公式.
(2)由a
n=n,
bn=4n,
cn=,知
S1=1<,
S2=1+=<,
S3=1++=<,當n>3時,
Sn=+++…+<1+
+
+
+…+
<
.
(3)當n≥2,k=1,2,…,2n-1時,有d
k+d
2n-k=
×[+]≥
0,由此能夠推導出對任意的n∈N
*,都有(2n-1)•d
n≤T
2n-1.
解答:解:(1)依題意點P
n的坐標為(x
n,y
n-1),
∴
yn+1=4xn+n=
4xn+1,
∴x
n+1=x
n+n,
∴x
n=x
n-1+n-1
=x
n-2+(n-2)+(n-1)
=…=x
1+1+2+…+(n-1)
=
+1.
(2)由(1)知,a
n=n,
bn=4n,
∵
cn=,
∴
S1=1<,
S2=1+=<,
S3=1++=<,
∴當n>3時,
Sn=+++…+<1+
+
+
+…+
=1+
+
×=
+-<
.
(3)當n≥2,k=1,2,…,2n-1時,有:
d
k+d
2n-k=
×[+]≥
×2=
=
,
又∵4
k+4
2n-k≥2×4
n,
∴4
2n-4
k-4
2n-k+1≤4
2n-2×4
n+1=(4
n-1)
2,
∴
dk+d2n-k≥×=2dn,
T2n-1≥×(2n-1)×2dn=(2n-1)d
n,
∴對任意的n∈N
*,都有(2n-1)•d
n≤T
2n-1.
點評:本題考查數列的通項公式的求法,考查兩個數大小的比較,考查不等式的證明,解題時要認真審題,注意等價轉化思想的合理運用.



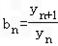 .
.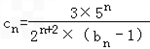 ,數列{cn}的前n項和為Tn,
,數列{cn}的前n項和為Tn, ;
;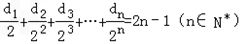 ,記數列{an}的前n項和為An,數列{dn}的前n項和為Bn,試比較An與
,記數列{an}的前n項和為An,數列{dn}的前n項和為Bn,試比較An與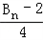 的大小.
的大小.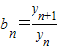 .
.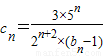 ,數列{cn}的前n項和為Tn,求證:
,數列{cn}的前n項和為Tn,求證: ;
;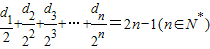 ,記數列{an}的前n項和為An,數列{dn}的前n項和為Bn,試比較An與
,記數列{an}的前n項和為An,數列{dn}的前n項和為Bn,試比較An與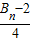 的大小.
的大小.