
【題目】目前,我國老年人口比例不斷上升,造成日趨嚴峻的人口老齡化問題.2019年10月12日,北京市老齡辦、市老齡協會聯合北京師范大學中國公益研究院發布《北京市老齡事業發展報告(2018)》,相關數據有如下圖表.規定年齡在15歲至59歲為“勞動年齡”,具備勞動力,60歲及以上年齡為“老年人”,據統計,2018年底北京市每2.4名勞動力撫養1名老年人.
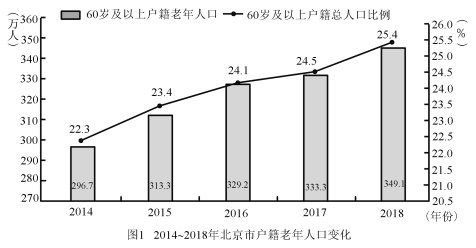
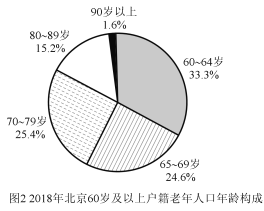
(Ⅰ)請根據上述圖表計算北京市2018年戶籍總人口數和北京市2018年的勞動力數;(保留兩位小數)
(Ⅱ)從2014年起,北京市老齡人口與年份呈線性關系,比照2018年戶籍老年人人口年齡構成,預計到2020年年底,北京市90以上老人達到多少人?(精確到1人)
(附:對于一組數據![]() 其回歸直線
其回歸直線![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為: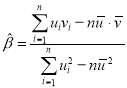 ,
,![]() .
.![]() ,
,![]() )
)
【答案】(Ⅰ)1374.41萬人837.84萬人(Ⅱ)59878人.
【解析】
(Ⅰ)由圖表數據及題意計算可得;
(Ⅱ)設2014年是第1年,第x年老年人口為y萬人,可得如下表格;依題意設![]() ,根據所給數據求出
,根據所給數據求出![]() ,
,![]() ,求出
,求出![]() 、
、![]() ,即可得得到回歸直線方程,再將
,即可得得到回歸直線方程,再將![]() 代入計算可得;
代入計算可得;
解:(Ⅰ)2018年北京市老年人349.1萬人,占戶籍總人口的25.4%,所以北京市2018年戶籍總人口![]() 萬人;
萬人;
2018年北京市“老年人”有349.1萬人,每2.4名勞動力撫養1名老年人,故北京市2018年的勞動力數為![]() 萬
萬
(Ⅱ)設2014年是第1年,第x年老年人口為y萬人,則
| 1 | 2 | 3 | 4 | 5 |
| 296.7 | 313.3 | 329.2 | 333.3 | 349.1 |
由于從2014年起,北京市老齡人口與年份呈線性關系,設![]()
則![]() ,
,![]() .
.
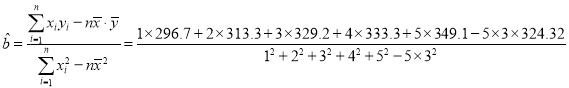
![]()
得![]()
∴![]()
當![]() 時,
時,![]()
∴北京市2020年年底的老年人人數約為374.24萬人,
90以上老人占1.6%,![]() 萬人≈59878人
萬人≈59878人
答:預計到2020年年底,北京市90以上老人約為59878人.


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:高中數學 來源: 題型:
【題目】在全民抗擊新冠肺炎疫情期間,北京市開展了“停課不停學”活動,此活動為學生提供了多種網絡課程資源以供選擇使用.活動開展一個月后,某學校隨機抽取了高三年級的甲、乙兩個班級進行網絡問卷調查,統計學生每天的學習時間,將樣本數據分成![]() 五組,并整理得到如下頻率分布直方圖:
五組,并整理得到如下頻率分布直方圖:
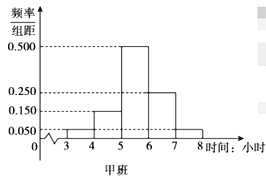
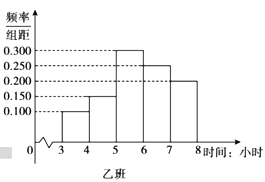
(1)已知該校高三年級共有600名學生,根據甲班的統計數據,估計該校高三年級每天學習時間達到5小時及以上的學生人數;
(2)已知這兩個班級各有40名學生,從甲、乙兩個班級每天學習時間不足4小時的學生中隨機抽取3人,記從甲班抽到的學生人數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)記甲、乙兩個班級學生每天學習時間的方差分別為![]() ,
,![]() ,試比較
,試比較![]() 與
與![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的右準線為直線
的右準線為直線![]() ,左頂點為
,左頂點為![]() ,右焦點為
,右焦點為![]() . 已知斜率為2的直線
. 已知斜率為2的直線![]() 經過點
經過點![]() ,與橢圓
,與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() 到直線
到直線![]() 的距離為
的距離為![]()
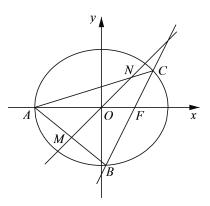
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若過![]() 的直線
的直線![]() 與直線
與直線![]() 分別相交于
分別相交于![]() 兩點,且
兩點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.在做回歸分析時,殘差圖中殘差點分布的帶狀區域的寬度越窄表示回歸效果越差
B.某地氣象局預報:6月9日本地降水概率為90%,結果這天沒下雨,這表明天氣預報并不科學
C.回歸分析模型中,殘差平方和越小,說明模型的擬合效果越好
D.在回歸直線方程![]() 中,當解釋變量每增加1個單位時,預報變量多增加0.1個單位
中,當解釋變量每增加1個單位時,預報變量多增加0.1個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面
的底面![]() 為平行四邊形,
為平行四邊形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
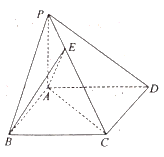
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)在側棱![]() 上是否存在點E,使
上是否存在點E,使![]() 與底面
與底面![]() 所成的角為45°?若存在,求
所成的角為45°?若存在,求![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某社會機構為了調查對手機游戲的興趣與年齡的關系,通過問卷調查,整理數據得如下![]() 列聯表:
列聯表:
40歲以下 | 40歲以上 | 合計 | |
很興趣 | 30 | 15 | 45 |
無興趣 | 20 | 35 | 55 |
合計 | 50 | 50 | 100 |
(1)根據列聯表,能否有![]() 的把握認為對手機游戲的興趣程度與年齡有關?
的把握認為對手機游戲的興趣程度與年齡有關?
(2)若已經從![]() 歲以下的被調查者中用分層抽樣的方式抽取了
歲以下的被調查者中用分層抽樣的方式抽取了![]() 名,現從這
名,現從這![]() 名被調查者中隨機選取
名被調查者中隨機選取![]() 名,求這
名,求這![]() 名被調查者中恰有
名被調查者中恰有![]() 名對手機游戲無興趣的概率.
名對手機游戲無興趣的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.84 | 6.635 | 10.828 |
(注:參考公式: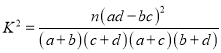 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機調查某城市80名有子女在讀小學的成年人,以研究晚上八點至十點時間段輔導子女作業與性別的關系,得到下面的數據表:
是否輔導 性別 | 輔導 | 不輔導 | 合計 |
男 | 25 | 60 | |
女 | |||
合計 | 40 | 80 |
(1)請將表中數據補充完整;
(2)用樣本的頻率估計總體的概率,估計這個城市有子女在讀小學的成人女性晚上八點至十點輔導子女作業的概率;
(3)根據以上數據,能否有99%以上的把握認為“晚上八點至十點時間段是否輔導子女作業與性別有關?”.
參考公式: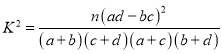 ,其中
,其中![]() .
.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】羽毛球比賽中,首局比賽由裁判員采用拋球的方法決定誰先發球,在每回合爭奪中,贏方得1分且獲得發球權.每一局中,獲勝規則如下:①率先得到21分的一方贏得該局比賽;②如果雙方得分出現![]() ,需要領先對方2分才算該局獲勝;③如果雙方得分出現
,需要領先對方2分才算該局獲勝;③如果雙方得分出現![]() ,先取得30分的一方該局獲勝.現甲、乙兩名運動員進行對抗賽,在每回合爭奪中,若甲發球時,甲得分的概率為
,先取得30分的一方該局獲勝.現甲、乙兩名運動員進行對抗賽,在每回合爭奪中,若甲發球時,甲得分的概率為![]() ;乙發球時,甲得分的概率為
;乙發球時,甲得分的概率為![]() .
.
(Ⅰ)若![]() ,記“甲以
,記“甲以![]() 贏一局”的概率為
贏一局”的概率為![]() ,試比較
,試比較![]() 與
與![]() 的大小;
的大小;
(Ⅱ)根據對以往甲、乙兩名運動員的比賽進行數據分析,得到如下![]() 列聯表部分數據.若不考慮其它因素對比賽的影響,并以表中兩人發球時甲得分的頻率作為
列聯表部分數據.若不考慮其它因素對比賽的影響,并以表中兩人發球時甲得分的頻率作為![]() ,
,![]() 的值.
的值.
甲得分 | 乙得分 | 總計 | |
甲發球 | 50 | 100 | |
乙發球 | 60 | 90 | |
總計 | 190 |
①完成![]() 列聯表,并判斷是否有95%的把握認為“比賽得分與接、發球有關”?
列聯表,并判斷是否有95%的把握認為“比賽得分與接、發球有關”?
②已知在某局比中,雙方戰成![]() ,且輪到乙發球,記雙方再戰
,且輪到乙發球,記雙方再戰![]() 回合此局比賽結束,求
回合此局比賽結束,求![]() 的分布列與期望.
的分布列與期望.
參考公式: ,其中
,其中![]() .
.
臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com