【題目】某服裝廠生產一種服裝，每件服裝的成本為40元，出廠單價為60元，該廠為鼓勵銷售商訂購，決定當一次訂購量超過100件時，每多訂購一件，訂購的全部服裝的出廠單價就降低0.02元，根據市場調查，銷售商一次訂購量不會超過500件．
（1）設一次訂購量為x件，服裝的實際出廠單價為P元，寫出函數P=f（x）的表達式；
（2）當銷售商一次訂購多少件服裝時，該服裝廠獲得的利潤最大？并求出最大值．
【答案】
（1）解：設一次訂購量為x件，服裝的實際出廠單價為P元，
當0＜x≤100時，P=60
當100＜x≤500時， 
所以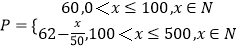 
（2）解：設銷售商一次訂購量為x件，工廠獲得的利潤為y元，則有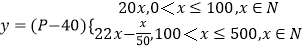 
當0＜x≤100且x∈N時，易知x=100，y取得最大值2000元
當100＜x≤500且x∈N時， 
，
則此函數在100＜x≤500且x∈N上遞增，故x=500時，y取得最大值6000元．
∵6000＞2000，
∴當銷售商一次訂購500件服裝時，該服裝廠獲得的最大利潤6000元
【解析】（1）利用分段函數直接列出函數的解析式即可．（2）利用（1）列出利潤函數，分別求解分段函數的最值，推出結果即可．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】對于任意實數a，b，c，d，以下四個命題中的真命題是（ ）
A.若a＞b，c≠0則ac＞bc
B.若a＞b＞o，c＞d則ac＞bd
C.若a＞b，則 
D.若ac2＞bc2則a＞b
查看答案和解析>>
科目：高中數學 來源： 題型：
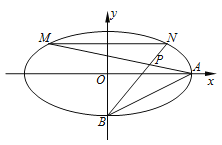
【題目】如圖，在平面直角坐標系
中，已知橢圓
過點
， 
， 
分別為橢圓
的右、下頂點，且
．
（1）求橢圓
的方程；
（2）設點
在橢圓
內，滿足直線
， 
的斜率乘積為
，且直線
， 
分別交橢圓
于點
， 
．
(i) 若
， 
關于
軸對稱，求直線
的斜率；
(ii) 求證： 
的面積與
的面積相等．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在棱長為1的正方體ABCD﹣A1B1C1D1中，點E，F分別是棱BC，CC1的中點，P是側面BCC1B1內一點，若A1P∥平面AEF，則線段A1P長度的取值范圍是 ．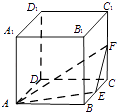 
查看答案和解析>>
科目：高中數學 來源： 題型：
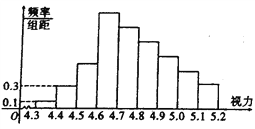
【題目】統計全國高三學生的視力情況，得到如圖所示的頻率分布直方圖，由于不慎將部分數據丟失，但知道前4組的頻率成等比數列，后6組的頻率成等差數列.
（Ⅰ）求出視力在[4.7,4.8]的頻率；
（Ⅱ）現從全國的高三學生中隨機地抽取4人，用
表示視力在[4.3,4.7]的學生人數，寫出
的分布列，并求出
的期望與方差.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數F（x）=g（x）+h（x）=ex ， 且g（x），h（x）分別是R上的偶函數和奇函數，若對任意的x∈（0，+∞），不等式g（2x）≥ah（x）恒成立，則實數a的取值范圍是（ ）
A.（﹣∞，2 
]
B.（﹣∞，2 ）
C.（﹣∞，2]
D.（﹣∞，2）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=﹣3x2+a（6﹣a）x+c．
（1）當c=19時，解關于a的不等式f（1）＞0；
（2）若關于x的不等式f（x）＞0的解集是（﹣1，3），求實數a，c的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的頂點為原點
，焦點為圓
的圓心
.經過點
的直線
交拋物線
于
兩點，交圓
于
兩點， 
在第一象限， 
在第四象限.
（1）求拋物線
的方程；
（2）是否存在直線
，使
是
與
的等差中項？若存在，求直線
的方程；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有甲、乙兩個班進行數學考試，按照大于等于120分為優秀，120分以下為非優秀統計成績后，得到如下
列聯表：（單位：人）.
已知在全部105人中隨機抽取1人成績是優秀的概率為
.
（1）請完成上面的
列聯表，并根據表中數據判斷，是否有
的把握認為“成績與班級有關系”？
（2）若甲班優秀學生中有男生6名，女生4名，現從中隨機選派3名學生參加全市數學競賽，記參加競賽的男生人數為
，求
的分布列與期望.
附：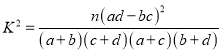 
| 0.15 | 0.10 | 0.050 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
