
【題目】對于兩個定義域相同的函數![]() 、
、![]() ,若存在實數
,若存在實數![]() 、
、![]() 使
使![]() ,則稱函數
,則稱函數![]() 是由“基函數
是由“基函數![]() 、
、![]() ”生成的.
”生成的.
(1)![]() 和
和![]() 生成一個偶函數
生成一個偶函數![]() ,求
,求![]() 的值;
的值;
(2)若![]() 由
由![]() ,
,![]() (
(![]() 且
且![]() )生成,求
)生成,求![]() 的取值范圍;
的取值范圍;
(3)試利用“基函數![]() ,
,![]() ”生成一個函數
”生成一個函數![]() ,使
,使![]() 滿足下列條件:①是偶函數;②有最小值1,請求出函數
滿足下列條件:①是偶函數;②有最小值1,請求出函數![]() 的解析式并進一步研究該函數的單調性(無需證明).
的解析式并進一步研究該函數的單調性(無需證明).
【答案】(1)0;(2)![]() ;(3)
;(3)![]() ,在
,在![]() 遞減,在
遞減,在![]() 遞增
遞增
【解析】
(1)由![]() 列方程,根據
列方程,根據![]() 為偶函數求得
為偶函數求得![]() 的關系式,進而求得
的關系式,進而求得![]() 的值.
的值.
(2)由![]() 列方程組,化簡后求得
列方程組,化簡后求得![]() 的關系式,利用導數求得
的關系式,利用導數求得![]() 的取值范圍.
的取值范圍.
(3)構造函數![]() ,并證得其奇偶性和單調性.
,并證得其奇偶性和單調性.
(1)由![]() 為偶函數可知
為偶函數可知![]() ,所以
,所以![]() .
.
(2)由![]() 得
得![]() ,所以
,所以 ,由于
,由于![]() ,所以可化簡得
,所以可化簡得![]() ,所以
,所以![]() .構造函數
.構造函數![]() ,
,![]() ,所以函數
,所以函數![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,所以函數在
上遞減,所以函數在![]() 處,有極大值
處,有極大值![]() ,在
,在![]() 處有極小值
處有極小值![]() .所以
.所以![]() 的取值范圍是
的取值范圍是![]() .
.
(3)構造函數![]() ,
,![]() ,所以
,所以![]() 為偶函數.由于
為偶函數.由于![]() ,所以
,所以![]() 有最小值
有最小值![]() 符合題意.
符合題意.![]() 在
在![]() 遞減,在
遞減,在![]() 遞增.
遞增.
另補證明:由于![]() 為偶函數,只需求得
為偶函數,只需求得![]() 上的單調性.構造函數
上的單調性.構造函數![]() ,
,![]() ,由于
,由于![]() 時,
時,![]() ,故
,故![]() ,所以函數
,所以函數![]() 在
在![]() 上遞增.根據復合函數單調性同增異減可知,函數
上遞增.根據復合函數單調性同增異減可知,函數![]() 在
在![]() 上遞增.根據
上遞增.根據![]() 為偶函數可知,函數
為偶函數可知,函數![]() 在
在![]() 遞減.
遞減.


科目:高中數學 來源: 題型:
【題目】已知![]() 是圓錐的高,
是圓錐的高,![]() 是圓錐底面的直徑,
是圓錐底面的直徑,![]() 是底面圓周上一點,
是底面圓周上一點,![]() 是
是![]() 的中點,平面
的中點,平面![]() 和平面
和平面![]() 將圓錐截去部分后的幾何體如圖所示.
將圓錐截去部分后的幾何體如圖所示.
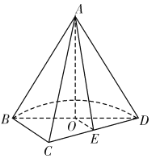
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國道路交通安全法》第47條的相關規定:機動車行經人行道時,應當減速慢行;遇行人正在通過人行道,應當停車讓行,俗稱“禮讓斑馬線”, 《中華人民共和國道路交通安全法》第90條規定:對不禮讓行人的駕駛員處以扣3分,罰款50元的處罰.下表是某市一主干路口監控設備所抓拍的5個月內駕駛員“禮讓斑馬線”行為統計數據:
月份 | 1 | 2 | 3 | 4 | 5 |
違章駕駛員人數 | 120 | 105 | 100 | 90 | 85 |
(1)請利用所給數據求違章人數![]() 與月份
與月份![]() 之間的回歸直線方程
之間的回歸直線方程![]() ;
;
(2)預測該路口9月份的不“禮讓斑馬線”違章駕駛員人數.
參考公式: 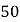 ,
, ![]() .
.
參考數據: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將數列![]() 的前n項和分成兩部分,且兩部分的項數分別是i,
的前n項和分成兩部分,且兩部分的項數分別是i,![]() ,若兩部分的和相等,則稱數列
,若兩部分的和相等,則稱數列![]() 的前n項和能夠進行
的前n項和能夠進行![]() 等和分割.
等和分割.
![]() 若
若![]() ,
,![]() ,試寫出數列
,試寫出數列![]() 的前4項和的所有等和分割;
的前4項和的所有等和分割;
![]() 求證:等差數列
求證:等差數列![]() 的前
的前![]() 項和能夠進行
項和能夠進行![]() 等和分割;
等和分割;
![]() 若數列
若數列![]() 的通項公式為:
的通項公式為:![]() ,且數列
,且數列![]() 的前n項和能進行等和分割,求所有滿足條件的n.
的前n項和能進行等和分割,求所有滿足條件的n.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 滿足
滿足![]() ,其中
,其中![]() ,且
,且![]() ,
, ![]() 為常數.
為常數.
(1)若![]() 是等差數列,且公差
是等差數列,且公差![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且存在
,且存在![]() ,使得
,使得![]() 對任意的
對任意的![]() 都成立,求
都成立,求![]() 的最小值;
的最小值;
(3)若![]() ,且數列
,且數列![]() 不是常數列,如果存在正整數
不是常數列,如果存在正整數![]() ,使得
,使得![]() 對任意的
對任意的![]() 均成立. 求所有滿足條件的數列
均成立. 求所有滿足條件的數列![]() 中
中![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點
的焦點![]() 恰好是橢圓
恰好是橢圓![]() 的右焦點.
的右焦點.
(1)求實數![]() 的值及拋物線
的值及拋物線![]() 的準線方程;
的準線方程;
(2)過點![]() 任作兩條互相垂直的直線分別交拋物線
任作兩條互相垂直的直線分別交拋物線![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() 點,求兩條弦的弦長之和
點,求兩條弦的弦長之和![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com