Question

如圖,在四棱錐P—ABCD中,頂點P在底面ABCD內的射影恰好落在AB的中點O上,又∠BAD=90°,BC∥AD,且BC∶AB∶AD=1∶2∶2.

(1)求證:PD⊥AC;

(2)若PO=BC,求直線PD與AB所成的角;

(3)若平面APB與平面PCD所成的角為60°,求的值.

Answer 1

解:因為AB中點O為點P在平面ABCD內的射影，所以PO⊥底面ABCD.以O為坐標原點,AB所在直線為x軸,OP所在直線為z軸,建立空間直角坐標系O—xyz(如圖).?

?

(1)    證明:設BC=a,OP=h,則依據題意B(a,0,0),A(-a,0,0),P(0,0,h),C(a,a,0),D(-a,2a,0).

∴=(2a,a,0),=(-a,2a,-h),于是·=-2a²+2a²=0.?

∴PD⊥AC.                                                                                                             ?

(2)由PO=BC，得h=a，于是P(0，0，a).?

∵=(2a,0,0),=(-a,2a,-a),?

∴·=-2a²,                                                                                           

?cos〈,〉== -.?

∴ 直線PD與AB所成的角的余弦值為.?

(3)設平面PAB的法向量為m，可得m=(0,1,0).?

設平面PCD的法向量為n=(x,y,z)，由PC=(a,a,-h),PD=(-a,2a,-h),?

∴ax+ay-hz=0,-ax+2ay-hz=0,解得n=(1,2,).?

∴m·n=2,?

cos〈m,n〉=.?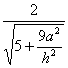

∵二面角為60°，?

∴=4.?

解得=,即=.