③④
分析:①曲線y=-x
2+2x+4在點(1,5)處的切線的傾斜角為45°,求出切點處的導數值,進行驗證;
②已知直線l,m,平面α,β,若l⊥α,m?β,l⊥m,則α∥β,由面面位置關系進行判斷;
③設函數f(x)=Asin(ωx+φ),(A>0,ω>0),若f(1)=0,則f(x+1)一定是奇函數,求出兩參數ω,φ的關系,整理解析式,觀察既得;
④如果點P到點
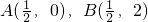
及直線

的距離相等,那么滿足條件的點P有且只有1個,由兩直線的交點個數研究即可.
解答:①曲線y=-x
2+2x+4在點(1,5)處的切線的傾斜角為45°.是錯誤命題,因為y′=-2x+2,在點(1,5)處的導數值為0,故傾斜角不是45°;
②已知直線l,m,平面α,β,若l⊥α,m?β,l⊥m,則α∥β是錯誤命題,在題設中的條件下,兩平面可以是相交的;
③設函數f(x)=Asin(ωx+φ),(A>0,ω>0),若f(1)=0,則f(x+1)一定是奇函數,是正確命題,由f(1)=0,得出ω+φ=0,函數解析式可變為f(x)=Asinω(x-1),左移一個單位可得到f(x)=Asinωx是一個奇函數;
④如果點P到點
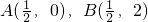
及直線

的距離相等,那么滿足條件的點P有且只有1個,是正確命題,作出兩點的垂直平分線y=1,與直線

相交,故滿足條件的點只有一個.
綜上③④是正確命題
故答案為③④
點評:本題考查奇函數,函數圖象的變換,導數的幾何意義等內容,解答本題的關鍵是對本題中命題所涉及到的相關知識點都比較熟悉,方能避免誤判.本題是考查雙基的題.

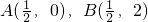 及直線
及直線 的距離相等,那么滿足條件的點P有且只有1個.
的距離相等,那么滿足條件的點P有且只有1個.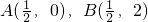 及直線
及直線 的距離相等,那么滿足條件的點P有且只有1個,由兩直線的交點個數研究即可.
的距離相等,那么滿足條件的點P有且只有1個,由兩直線的交點個數研究即可.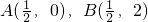 及直線
及直線 的距離相等,那么滿足條件的點P有且只有1個,是正確命題,作出兩點的垂直平分線y=1,與直線
的距離相等,那么滿足條件的點P有且只有1個,是正確命題,作出兩點的垂直平分線y=1,與直線 相交,故滿足條件的點只有一個.
相交,故滿足條件的點只有一個.

 閱讀快車系列答案
閱讀快車系列答案