【題目】已知圓M的圓心在直線
：
上，與直線
：
相切，截直線
：
所得的弦長為6.
（1）求圓M的方程；
（2）過點
的兩條成
角的直線分別交圓M于A，C和B，D，求四邊形
面積的最大值.
【答案】（1）
（2）
【解析】
（1）設(shè)圓的標(biāo)準(zhǔn)方程，將圓心代入直線
的方程，由點到直線距離公式求得圓M到
的距離，由弦長公式及點到直線距離公式表示出直線
與圓的關(guān)系，解方程組即可求得
的值，即可求得圓M的標(biāo)準(zhǔn)方程
（2）解法1：作
，
，令
，
，討論
或
兩種情況：當(dāng)時，由余弦定理表示出
，而
、
、
、
四點共圓，根據(jù)正弦定理求得
，進而求得，結(jié)合基本不等式即可求得
，即可求得四邊形
面積的最大值；當(dāng)時，由基本不等式求得
，即可由二次函數(shù)性質(zhì)求得四邊形面積的最大值.
解法2：結(jié)合三角形面積公式可得
，由基本不等式可知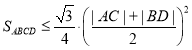
，討論或兩種情況，即可確定四邊形面積的最大值.
（1）設(shè)圓M的方程為：
則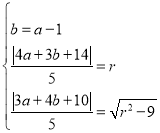
，解得：
，
∴所求圓方程為
（2）解法1：
如圖作，，令，，或
當(dāng)時，
，
因、、、四點共圓，
由正弦定理
，
∴
，
又
，
∴，
，
，當(dāng)且僅當(dāng)
時取等，
當(dāng)時，
，
∴，
又
，
所以
，
綜上所述，四邊形面積的最大值為.
解法2：
（當(dāng)且僅當(dāng)
時取等號），
要使得，則直線PM應(yīng)是
的平分線，
當(dāng)
時，圓心M到直線AC、BD的距離為
，則
，
.
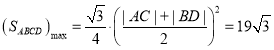當(dāng)
時，圓心M到直線AC、BD的距離為
，則
，
.
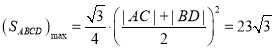綜上所述，四邊形面積的最大值為.
課前課后同步練習(xí)系列答案
課堂小作業(yè)系列答案
黃岡小狀元口算速算練習(xí)冊系列答案
成功訓(xùn)練計劃系列答案
倍速訓(xùn)練法直通中考考點系列答案
一卷搞定系列答案
名校作業(yè)本系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】某校高三課外興趣小組為了解高三同學(xué)高考結(jié)束后是否打算觀看2018年足球世界杯比賽的情況,從全校高三年級1500名男生、1000名女生中按分層抽樣的方式抽取125名學(xué)生進行問卷調(diào)查,情況如下表:
打算觀看 | 不打算觀看 | |
女生 | 20 | b |
男生 | c | 25 |
（1）求出表中數(shù)據(jù)b，c;
（2）判斷是否有99%的把握認(rèn)為觀看2018年足球世界杯比賽與性別有關(guān);
（3）為了計算“從10人中選出9人參加比賽”的情況有多少種，我們可以發(fā)現(xiàn)它與“從10人中選出1人不參加比賽”的情況有多少種是一致的.現(xiàn)有問題：在打算觀看2018年足球世界杯比賽的同學(xué)中有5名男生、2名女生來自高三（5）班，從中推選5人接受校園電視臺采訪，請根據(jù)上述方法，求被推選出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附： 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
是偶函數(shù)，且滿足
，當(dāng)
時， 
，當(dāng)
時， 
的最大值為
.
（1）求實數(shù)
的值；
（2）函數(shù)
，若對任意的
，總存在
，使不等式
恒成立，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
： 
的左、右焦點分別為
， 
，且離心率為
， 
為橢圓上任意一點，當(dāng)
時， 
的面積為1.
（1）求橢圓
的方程；
（2）已知點
是橢圓
上異于橢圓頂點的一點，延長直線
， 
分別與橢圓交于點
， 
，設(shè)直線
的斜率為
，直線
的斜率為
，求證： 
為定值.
【答案】（1）
；（2）
【解析】試題分析：（1）設(shè)
由題
，由此求出
,可得橢圓
的方程；
（2）設(shè)
， 
，
當(dāng)直線
的斜率不存在時，可得
；
當(dāng)直線
的斜率不存在時，同理可得
.
當(dāng)直線
、
的斜率存在時，
，
設(shè)直線
的方程為
，則由
消去
通過運算可得
，同理可得
，由此得到直線
的斜率為
，
直線
的斜率為
，進而可得
.
試題解析：（1）設(shè)由題
，
解得
，則
，
橢圓
的方程為
.
（2）設(shè)
， 
，
當(dāng)直線
的斜率不存在時，設(shè)
，則
，
直線
的方程為
代入
，可得
，
， 
，則
，
直線
的斜率為
，直線
的斜率為
，
，
當(dāng)直線
的斜率不存在時，同理可得
.
當(dāng)直線
、
的斜率存在時，，
設(shè)直線
的方程為
，則由
消去
可得：
，
又
，則
，代入上述方程可得
，
，則
，
設(shè)直線
的方程為
，同理可得
，
直線
的斜率為
，
直線
的斜率為
，
.
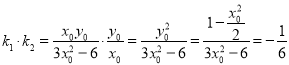所以，直線
與
的斜率之積為定值
，即
.
【題型】解答題
【結(jié)束】
21
【題目】已知函數(shù)
， 
，在
處的切線方程為
.
（1）求
， 
；
（2）若
，證明： 
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，曲線
的參數(shù)方程為
（
， 
為參數(shù)），以坐標(biāo)原點
為極點， 
軸正半軸為極軸建立極坐標(biāo)系，直線
的極坐標(biāo)方程為
，若直線
與曲線
相切；
（1）求曲線
的極坐標(biāo)方程；
（2）在曲線
上取兩點
， 
與原點
構(gòu)成
，且滿足
，求面積
的最大值.
【答案】（1）
；（2）
【解析】試題分析：（1）利用極坐標(biāo)與直角坐標(biāo)的互化公式可得直線
的直角坐標(biāo)方程為
，
，消去參數(shù)
可知曲線
是圓心為
，半徑為
的圓，由直線
與曲線
相切，可得： 
；則曲線C的方程為
， 再次利用極坐標(biāo)與直角坐標(biāo)的互化公式可得
可得曲線C的極坐標(biāo)方程.
(2)由（1）不妨設(shè)M（
），
，（
），
，
，
由此可求
面積的最大值.
試題解析：（1）由題意可知直線
的直角坐標(biāo)方程為
，
曲線
是圓心為
，半徑為
的圓，直線
與曲線
相切，可得： 
；可知曲線C的方程為
，
所以曲線C的極坐標(biāo)方程為
，
即
.
(2)由（1）不妨設(shè)M（
），，（
），
，
，
當(dāng)
時， 
，
所以△MON面積的最大值為
.
【題型】解答題
【結(jié)束】
23
【題目】已知函數(shù)
的定義域為
；
（1）求實數(shù)
的取值范圍；
（2）設(shè)實數(shù)
為
的最大值，若實數(shù)
， 
， 
滿足
，求
的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】對某校高三年級學(xué)生參加社區(qū)服務(wù)次數(shù)進行統(tǒng)計，隨機抽取M名學(xué)生作為樣本，得到這M名學(xué)生參加社區(qū)服務(wù)的次數(shù)．根據(jù)此數(shù)據(jù)作出了頻數(shù)與頻率的統(tǒng)計表如下，頻率分布直方圖如圖：
分組 | 頻數(shù) | 頻率 |
[10，15） | 10 | 0.25 |
[15，20） | 24 | n |
[20，25） | m | p |
[25，30） | 2 | 0.05 |
合計 | M | 1 |
（1）求出表中M，p及圖中a的值；
（2）若該校高三學(xué)生有240人，試估計該校高三學(xué)生參加社區(qū)服務(wù)的次數(shù)在區(qū)間[10，15）內(nèi)的人數(shù)；
（3）在所取樣本中，從參加社區(qū)服務(wù)的次數(shù)不少于20次的學(xué)生中任選2人，求至多一人參加社區(qū)服務(wù)次數(shù)在區(qū)間[25，30）內(nèi)的概率．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某射擊運動員進行射擊訓(xùn)練，前三次射擊在靶上的著彈點
剛好是邊長為
的等邊三角形的三個頂點.
（Ⅰ）第四次射擊時，該運動員瞄準(zhǔn)
區(qū)域射擊（不會打到外），則此次射擊的著彈點距的距離都超過
的概率為多少？（彈孔大小忽略不計）
(Ⅱ) 該運動員前三次射擊的成績（環(huán)數(shù)）都在區(qū)間
內(nèi)，調(diào)整一下后，又連打三槍，其成績（環(huán)數(shù)）都在區(qū)間
內(nèi).現(xiàn)從這
次射擊成績中隨機抽取兩次射擊的成績（記為
和
）進行技術(shù)分析.求事件“
”的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為了配合新冠疫情防控，某市組織了以“停課不停學(xué)，成長不停歇”為主題的“空中課堂”，為了了解一周內(nèi)學(xué)生的線上學(xué)習(xí)情況，從該市中抽取1000名學(xué)生進行調(diào)査，根據(jù)所得信息制作了如圖所示的頻率分布直方圖．
（1）為了估計從該市任意抽取的3名同學(xué)中恰有2人線上學(xué)習(xí)時間在[200,300）的概率
，特設(shè)計如下隨機模擬的方法：先由計算器產(chǎn)生0到9之間取整數(shù)值的隨機數(shù)，依次用0,1,2,3，…9的前若干個數(shù)字表示線上學(xué)習(xí)時間在[200,300）的同學(xué)，剩余的數(shù)字表示線上學(xué)習(xí)時間不在[200,300）的同學(xué)；再以每三個隨機數(shù)為一組，代表線上學(xué)習(xí)的情況．
假設(shè)用上述隨機模擬方法已產(chǎn)生了表中的30組隨機數(shù)，請根據(jù)這批隨機數(shù)估計概率的值；
907 966 191 925 271 569 812 458 932 683 431 257 027 556
438 873 730 113 669 206 232 433 474 537 679 138 602 231
（2）為了進一步進行調(diào)查，用分層抽樣的方法從這1000名學(xué)生中抽出20名同學(xué)，在抽取的20人中，再從線上學(xué)習(xí)時間[350,450）（350分鐘至450分鐘之間）的同學(xué)中任意選擇兩名，求這兩名同學(xué)來自同一組的概率．
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
