
| |||||||||||||||
(1) |
解法一:∵正方形ABCD,∴CB⊥AB. ∵二面角C—AB—F是直二面角, CB⊥AB,∴CB⊥面ABEF. ∵AG,GB ∴CB⊥AG,CB⊥BG. 又AD=2a,AF=a,ABEF是矩形, G是EF的中點,
∴AG=BG= ∴AG⊥BG. ∵CB∩BG=B,∴AG⊥平面CBG, 而AG 如圖,以A為原點建立直角坐標系, 則A(0,0,0),B(0,2a,0), C(0,2a,2a),G(a,a,0), F(a,0,0).
∴
∴AG=⊥BG,AG⊥BC,而BG與BC是平面BCG內兩相交直線, ∴AG⊥平面BCG,又AG |
(2) |
解法一:如圖,由(1)知面ACG⊥面BGC,且交于GC,在平面BGC內作BH⊥GC,垂足為H,則BH⊥平面AGC. ∴∠BGH是BG與平面AGC所成的角, ∴在Rt△CBG中 BH= 又BG= 解法二:設GB與平面AGC所成角為θ. 由題意可得 設平面AGC的一個法向量為n=(x,y,1), 由
(或:在證出 得cos< |
(3) |
解法一:由(2),BH⊥面AGC.作BO⊥AC,垂足為0,連結HO,則HO⊥AC, ∴∠BOH為二面角B—AC—G的平面角. ∵在Rt△ABC中,BO= ∴在Rt△BOH中, 即二面角B—AC—G的大小為arcsin 解法二:因n=(1,-1,1)是平面AGC的一個法向量, 又AF⊥平面ABCD,平面ABCD的一個法向量 ∴設n與 ∴二面角B—AC—G的大小為arccos |


科目:高中數學 來源: 題型:
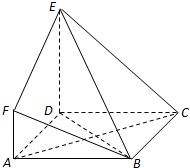 如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.
如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,ABCD是邊長為a的菱形,且∠BAD=60°,△PAD為正三角形,且面PAD⊥面ABCD.
如圖,ABCD是邊長為a的菱形,且∠BAD=60°,△PAD為正三角形,且面PAD⊥面ABCD.| AB |
| PD |
| EF |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,ABCD是邊長為2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是線段AD的中點,三棱錐F-OBC的體積為
如圖,ABCD是邊長為2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是線段AD的中點,三棱錐F-OBC的體積為| 2 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•寧城縣模擬)如圖,ABCD是邊長為1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.
(2012•寧城縣模擬)如圖,ABCD是邊長為1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,ABCD是邊長為2的正方形紙片,沿某動直線l為折痕將正方形在其下方的部分向上翻折,使得每次翻折后點B都落在邊AD上,記為B';折痕與AB交于點E,以EB和EB’為鄰邊作平行四邊形EB’MB.若以B為原點,BC所在直線為x軸建立直角坐標系(如下圖):
如圖,ABCD是邊長為2的正方形紙片,沿某動直線l為折痕將正方形在其下方的部分向上翻折,使得每次翻折后點B都落在邊AD上,記為B';折痕與AB交于點E,以EB和EB’為鄰邊作平行四邊形EB’MB.若以B為原點,BC所在直線為x軸建立直角坐標系(如下圖):查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com