【題目】等差數列{an}的前n項和為Sn ． 已知S3=a22 ， 且S1 ， S2 ， S4成等比數列，求{an}的通項式．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
，a為常數且a＞0．
（1）f（x）的圖象關于直線x= 
對稱；
（2）若x0滿足f（f（x0））=x0 ， 但f（x0）≠x0 ， 則x0稱為函數f（x）的二階周期點，如果f（x）有兩個二階周期點x1 ， x2 ， 試確定a的取值范圍；
（3）對于（2）中的x1 ， x2 ， 和a，設x3為函數f（f（x））的最大值點，A（x1 ， f（f（x1））），B（x2 ， f（f（x2））），C（x3 ， 0），記△ABC的面積為S（a），討論S（a）的單調性．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于棱長為
的正方體
，有如下結論，其中錯誤的是（ ）
A. 以正方體的頂點為頂點的幾何體可以是每個面都為直角三角形的四面體；
B. 過點
作平面
的垂線，垂足為點
，則
三點共線；
C. 過正方體中心的截面圖形不可能是正六邊形；
D. 三棱錐
與正方體的體積之比為
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（選修4﹣4：坐標系與參數方程）
已知曲線C1的參數方程為 
（t為參數），以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，曲線C2的極坐標方程為ρ=2sinθ．
（1）把C1的參數方程化為極坐標方程；
（2）求C1與C2交點的極坐標（ρ≥0，0≤θ＜2π）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高二文科分四個班，各班人數恰好成等差數列，高二數學調研測試后，對四個文科班的學生試卷按每班人數進行分層抽樣，對測試成績進行統計，人數最少的班抽取了
人，抽取的所有學生成績分為
組：
，
，
，
，
，
，得到如圖所示的頻率分布直方圖，其中第六組分數段的人數為
人．
（
）求
的值，并求出各班抽取的學生數各為多少人？
（
）在抽取的學生中，任取一名學生，求分數不小于
分的概率（視頻率為概率）．
（
）估計高二文科四個班數學成績的平均分
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國倉儲指數是反映倉儲行業經營和國內市場主要商品供求狀況與變化趨勢的一套指數體系．如圖所示的折線圖是2017年和2018年的中國倉儲指數走勢情況．根據該折線圖，下列結論中不正確的是（ ）
A. 2018年1月至4月的倉儲指數比2017年同期波動性更大
B. 2017年、2018年的最大倉儲指數都出現在4月份
C. 2018年全年倉儲指數平均值明顯低于2017年
D. 2018年各月倉儲指數的中位數與2017年各月倉儲指數中位數差異明顯
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線C： 
=1（a＞0，b＞0）的左、右焦點分別為F1 ， F2 ， 離心率為3，直線y=2與C的兩個交點間的距離為 
．
（1）求a，b；
（2）設過F2的直線l與C的左、右兩支分別相交于A、B兩點，且|AF1|=|BF1|，證明：|AF2|、|AB|、|BF2|成等比數列．
查看答案和解析>>
科目：高中數學 來源： 題型：
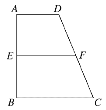
【題目】如圖梯形ABCD中，AD∥BC，∠ABC＝90°，AD∶BC∶AB＝2∶3∶4，E，F分別是AB，CD的中點,將四邊形ADFE沿直線EF進行翻折，給出四個結論：①DF⊥BC；
②BD⊥FC；
③平面DBF⊥平面BFC；
④平面DCF⊥平面BFC.
則在翻折過程中，可能成立的結論的個數為( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，
三個警亭有直道相通，已知
在
的正北方向6千米處，
在的正東方向
千米處.
（1）警員甲從出發，沿
行至點
處，此時
，求
的距離；
（2）警員甲從出發沿前往，警員乙從出發沿
前往，兩人同時出發，甲的速度為3千米/小時，乙的速度為6千米/小時.兩人通過專用對講機保持聯系，乙到達后原地等待，直到甲到達時任務結束.若對講機的有效通話距離不超過9千米，試問兩人通過對講機能保持聯系的總時長？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
