
如圖,在平面直角坐標(biāo)系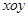 中,設(shè)點
中,設(shè)點 (
( ),直線
),直線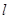 :
: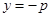 ,點
,點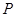 在直線
在直線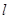 上移動,
上移動,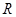 是線段
是線段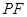 與
與 軸的交點, 過
軸的交點, 過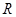 、
、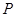 分別作直線
分別作直線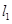 、
、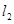 ,使
,使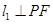 ,
,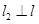
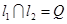 .
.

(1)求動點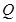 的軌跡
的軌跡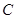 的方程;
的方程;
(2)在直線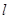 上任取一點
上任取一點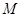 做曲線
做曲線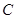 的兩條切線,設(shè)切點為
的兩條切線,設(shè)切點為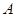 、
、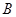 ,求證:直線
,求證:直線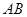 恒過一定點;
恒過一定點;
(3)對(2)求證:當(dāng)直線 的斜率存在時,直線
的斜率存在時,直線 的斜率的倒數(shù)成等差數(shù)列.
的斜率的倒數(shù)成等差數(shù)列.
(1) .(2)利用導(dǎo)數(shù)法求出直線AB的方程,然后再利用直線橫過定點知識解決.(3)用坐標(biāo)表示出斜率,然后再利用等差中項的知識證明即可
.(2)利用導(dǎo)數(shù)法求出直線AB的方程,然后再利用直線橫過定點知識解決.(3)用坐標(biāo)表示出斜率,然后再利用等差中項的知識證明即可
【解析】
試題分析:(1)依題意知,點 是線段
是線段 的中點,且
的中點,且 ⊥
⊥ ,
,
∴ 是線段
是線段 的垂直平分線.∴
的垂直平分線.∴ .
.
故動點 的軌跡
的軌跡 是以
是以 為焦點,
為焦點, 為準(zhǔn)線的拋物線,其方程為:
為準(zhǔn)線的拋物線,其方程為: .
.
(2)設(shè) ,兩切點為
,兩切點為 ,
,
由 得
得 ,求導(dǎo)得
,求導(dǎo)得 .
.
∴兩條切線方程為 ①
①
 ②
②
對于方程①,代入點 得,
得, ,又
,又
∴ 整理得:
整理得:
同理對方程②有
即 為方程
為方程 的兩根.
的兩根.
∴ ③
③
設(shè)直線 的斜率為
的斜率為 ,
,
所以直線 的方程為
的方程為 ,展開得:
,展開得:
 ,代入③得:
,代入③得:
∴直線恒過定點 .
.
(3) 證明:由(2)的結(jié)論,設(shè) ,
,  ,
,
且有 ,
,
∴
∴

=
又∵ ,所以
,所以
即直線 的斜率倒數(shù)成等差數(shù)列.
的斜率倒數(shù)成等差數(shù)列.
考點:本題考查了拋物線與導(dǎo)數(shù)、數(shù)列的綜合考查
點評:解答拋物線綜合題時,應(yīng)根據(jù)其幾何特征熟練的轉(zhuǎn)化為數(shù)量關(guān)系(如方程、函數(shù)),再結(jié)合代數(shù)方法解答,這就要學(xué)生在解決問題時要充分利用數(shù)形結(jié)合、設(shè)而不求、弦長公式及韋達(dá)定理綜合思考,重視對稱思想、函數(shù)與方程思想、等價轉(zhuǎn)化思想的應(yīng)用


科目:高中數(shù)學(xué) 來源: 題型:
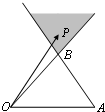 如圖,在△OAB中,點P是線段OB及線段AB延長線所圍成的陰影區(qū)域(含邊界)的任意一點,且
如圖,在△OAB中,點P是線段OB及線段AB延長線所圍成的陰影區(qū)域(含邊界)的任意一點,且| OP |
| OA |
| OB |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 1、如圖,在直角坐標(biāo)平面內(nèi)有一個邊長為a,中心在原點O的正六邊形ABCDEF,AB∥Ox.直線L:y=kx+t(k為常數(shù))與正六邊形交于M、N兩點,記△OMN的面積為S,則函數(shù)S=f(t)的奇偶性為
1、如圖,在直角坐標(biāo)平面內(nèi)有一個邊長為a,中心在原點O的正六邊形ABCDEF,AB∥Ox.直線L:y=kx+t(k為常數(shù))與正六邊形交于M、N兩點,記△OMN的面積為S,則函數(shù)S=f(t)的奇偶性為
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
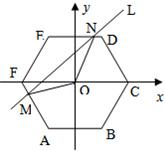 如圖,在直角坐標(biāo)平面內(nèi)有一個邊長為a、中心在原點O的正六邊形ABCDEF,AB∥Ox.直線L:y=kx+t(k為常數(shù))與正六邊形交于M、N兩點,記△OMN的面積為S,則函數(shù)S=f(t)的奇偶性為( )
如圖,在直角坐標(biāo)平面內(nèi)有一個邊長為a、中心在原點O的正六邊形ABCDEF,AB∥Ox.直線L:y=kx+t(k為常數(shù))與正六邊形交于M、N兩點,記△OMN的面積為S,則函數(shù)S=f(t)的奇偶性為( )| A、偶函數(shù) | B、奇函數(shù) | C、不是奇函數(shù),也不是偶函數(shù) | D、奇偶性與k有關(guān) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (2008•海珠區(qū)一模)如圖,在直角坐標(biāo)平面內(nèi),射線OT落在60°的終邊上,任作一條射線OA,OA落在∠xOT內(nèi)的概率是
(2008•海珠區(qū)一模)如圖,在直角坐標(biāo)平面內(nèi),射線OT落在60°的終邊上,任作一條射線OA,OA落在∠xOT內(nèi)的概率是| 1 |
| 6 |
| 1 |
| 6 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:

試問:是否存在定點E、F,使|ME|、|MB|、|MF|成等差數(shù)列?若存在,求出E、F的坐標(biāo);若不存在,說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com