下列四個命題中的假命題是( )
A.存在這樣的α、β,使得cos(α+β)=cosαcosβ-sinαsinβ
B.不存在無窮多個α、β,使得cos(α+β)=cosαcosβ-sinαsinβ
C.對于任意的α、β,cos(α+β)=cosαcosβ-sinαsinβ
D.不存在這樣的α、β,使得cos(α+β)≠cosαcosβ-sinαsinβ
【答案】分析:對A,由兩角和的余弦定理可知存在這樣的α、β,使得cos(α+β)=cosαcosβ+sinαsinβ,即可判斷;
對B,由cos(α+β)=cosαcosβ+sinαsinβ=cosαcosβ-sinαsinβ,得sinαsinβ=0.∴α=kπ或β=kπ(k∈Z),即可判斷;
對C,對于任意的α、β,cos(α+β)=cosαcosβ-sinαsinβ,即可得出答案;
對D,不存在這樣的α、β,使得cos(α+β)≠cosαcosβ-sinαsinβ,即可判斷真假;
解答:解:對A,由兩角和的余弦定理可知存在這樣的α、β,使得cos(α+β)=cosαcosβ+sinαsinβ,故本選項為真命題;
對B,由cos(α+β)=cosαcosβ+sinαsinβ=cosαcosβ-sinαsinβ,得sinαsinβ=0.∴α=kπ或β=kπ(k∈Z),故本選項為假命題.
對C,對于任意的α、β,由兩角和的余弦公式可得:cos(α+β)=cosαcosβ-sinαsinβ,故本選項為真命題;
對D,不存在這樣的α、β,使得cos(α+β)≠cosαcosβ-sinαsinβ,若存在α,β,則與兩角和的余弦公式矛盾,故本選項為真命題;
故選B.
點評:本題考查了四種命題的真假關系及兩角和與差的余弦函數,屬于基礎題,關鍵是掌握兩角和的余弦函數公式.



 是等差數列
是等差數列 的前n項和,且
的前n項和,且 ,有下列四個命
,有下列四個命 ; B.在所有
; B.在所有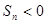 中,
中, 最大;
最大;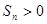 的
的 的個數有11個; D.
的個數有11個; D. ;
;