
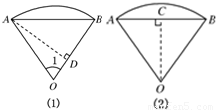
 解:法一:設扇形的半徑為r,弧長為l,則由已知可得
解:法一:設扇形的半徑為r,弧長為l,則由已知可得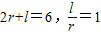 ,解得r=2,l=2.
,解得r=2,l=2. l•r=2.
l•r=2. OB•AD=
OB•AD= ×2×2sin 1=2sin 1,
×2×2sin 1=2sin 1, rad,所以OC=2cos
rad,所以OC=2cos  ,且AC=OA•sin
,且AC=OA•sin  =2sin
=2sin  ,
, AB•OC=
AB•OC= •2AC•OC=
•2AC•OC= •4sin
•4sin  •2cos
•2cos  =4sin
=4sin  •cos
•cos  ,
, •cos
•cos  .
.

 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源:福建省三明一中2012屆高三第二次學段考數學理科試題 題型:013
已知扇形的周長為
6 cm,面積是2 cm2,則扇形的圓心角的弧度數是1
4
1
或42
或4查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com