
【題目】如圖,多面體![]() 是正三棱柱(底面是正三角形的直棱柱)
是正三棱柱(底面是正三角形的直棱柱)![]() 沿平面
沿平面![]() 切除一部分所得,其中平面
切除一部分所得,其中平面![]() 為原正三棱柱的底面,
為原正三棱柱的底面,![]() ,點D為
,點D為![]() 的中點.
的中點.
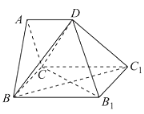
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)設![]() 與
與![]() 交于點E,連接
交于點E,連接![]() 、
、![]() ,由題意可得四邊形
,由題意可得四邊形![]() 是正方形,且
是正方形,且![]() ,再由點D為
,再由點D為![]() 的中點,
的中點,![]() 平行且等于
平行且等于![]() ,求得CD,同理求得
,求得CD,同理求得![]() ,得
,得![]() ,可得
,可得![]() ,由線面垂直的判定可得;
,由線面垂直的判定可得;
(2)取BC的中點O,連接AO,可得AO⊥BC,由正棱柱的性質可得AO⊥平面![]() ,以O為坐標原點,向量
,以O為坐標原點,向量![]() 、
、![]() 、
、![]() 分別為x、y,z軸建立空間直角坐標系,分別求出平面CBD與平面
分別為x、y,z軸建立空間直角坐標系,分別求出平面CBD與平面![]() 的一個法向量,由兩法向量所成角的余弦值可得二面角
的一個法向量,由兩法向量所成角的余弦值可得二面角![]() 的平面角的余弦值.
的平面角的余弦值.
(1)設![]() 與
與![]() 交于點E,連接
交于點E,連接![]() 、
、![]() .
.
∵多面體![]() 是正三棱柱沿平面
是正三棱柱沿平面![]() 切除部分所得,
切除部分所得,![]() ,
,
∴四邊形![]() 是正方形,且
是正方形,且![]() .
.
∵點D為![]() 的中點,
的中點,![]() 平行且等于
平行且等于![]() ,
,
∴![]() .
.
同理![]() ,
,
∴![]() .
.
∵E為![]() 的中點,
的中點,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ;
;
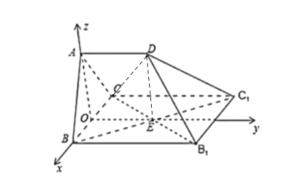
(2)取![]() 的中點O,連接
的中點O,連接![]() .
.
∵![]() 為正三角形,
為正三角形,![]() .
.
由正棱柱的性質可得,平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
以點O為原點,向量![]() 、
、![]() 、
、![]() 分別為x、y,z軸正方向建立如圖所示空間直角坐標系
分別為x、y,z軸正方向建立如圖所示空間直角坐標系![]() .
.
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則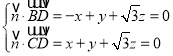 ,
,
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
由(1)可知,平面![]() 的一個法向量為
的一個法向量為![]() .
.
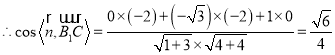 ,
,
又∵二面角![]() 的平面角為銳角,
的平面角為銳角,
∴二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
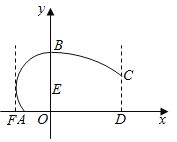
【題目】某地擬建造一座大型體育館,其設計方案側面的外輪廓如圖所示,曲線![]() 是以點
是以點![]() 為圓心的圓的一部分,其中
為圓心的圓的一部分,其中![]() ;曲線
;曲線![]() 是拋物線
是拋物線![]() 的一部分;
的一部分;![]() ,且
,且![]() 恰好等于圓
恰好等于圓![]() 的半徑.假定擬建體育館的高
的半徑.假定擬建體育館的高![]() (單位:米,下同).
(單位:米,下同).
(1)若![]() ,
,![]() ,求
,求![]() 、
、![]() 的長度;
的長度;
(2)若要求體育館側面的最大寬度![]() 不超過
不超過![]() 米,求
米,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABCA1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2,![]() =λ
=λ![]() .
.
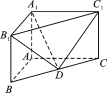
(1)若λ=1,求直線DB1與平面A1C1D所成角的正弦值;
(2)若二面角B1- A1C1-D的大小為60°,求實數λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌奶茶公司計劃在A地開設若干個連鎖加盟店,經調查研究,加盟店的個數x與平均每個店的月營業額y(萬元)具有如下表所示的數據關系:
x | 2 | 4 | 6 | 8 | 10 |
y | 20.9 | 20.2 | 19 | 17.8 | 17.1 |
(1)求y關于x的線性回歸方程;
(2)根據(1)中的結果分析,為了保證平均每個加盟店的月營業額不少于14.6萬元,則A地開設加盟店的個數不能超過幾個?
參考公式:線性回歸方程![]() 中的斜率和截距的最小二乘估計公式分別為
中的斜率和截距的最小二乘估計公式分別為
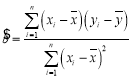 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() :
:![]() 的焦距為
的焦距為![]() ,直線
,直線![]() 截圓
截圓![]() :
:![]() 與橢圓
與橢圓![]() 所得的弦長之比為
所得的弦長之比為![]() ,橢圓
,橢圓![]() 與
與![]() 軸正半軸的交點分別為
軸正半軸的交點分別為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設點![]() (
(![]() 且
且![]() )為橢圓
)為橢圓![]() 上一點,點
上一點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,直線
,直線![]() ,
,![]() 分別交
分別交![]() 軸于點
軸于點![]() ,
,![]() .試判斷
.試判斷![]() 是否為定值?若是求出該定值,若不是定值,請說明理由.
是否為定值?若是求出該定值,若不是定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
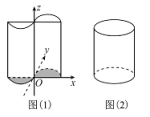
【題目】我國古代數學家祖暅提出原理:“冪勢既同,則積不容異”.其中“冪”是截面積,“勢”是幾何體的高.原理的意思是:夾在兩個平行平面間的兩個幾何體,被任一平行于這兩個平行平面的平面所截,若所截的兩個截面的面積恒相等,則這兩個幾何體的體積相等.如圖(1),函數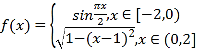 的圖象與x軸圍成一個封閉區域A(陰影部分),將區域A(陰影部分)沿z軸的正方向上移6個單位,得到一幾何體.現有一個與之等高的底面為橢圓的柱體如圖(2)所示,其底面積與區域A(陰影部分)的面積相等,則此柱體的體積為______.
的圖象與x軸圍成一個封閉區域A(陰影部分),將區域A(陰影部分)沿z軸的正方向上移6個單位,得到一幾何體.現有一個與之等高的底面為橢圓的柱體如圖(2)所示,其底面積與區域A(陰影部分)的面積相等,則此柱體的體積為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,BO、AO、CO所在直線兩兩垂直,且AO=CO,∠BAO=60°,E是AC的中點,三棱錐
中,BO、AO、CO所在直線兩兩垂直,且AO=CO,∠BAO=60°,E是AC的中點,三棱錐![]() 的體積為
的體積為![]()
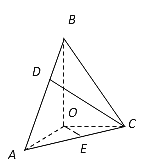
(1)求三棱錐![]() 的高;
的高;
(2)在線段AB上取一點D,當D在什么位置時,![]() 和
和![]() 的夾角大小為
的夾角大小為 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】華為董事會決定投資開發新款軟件,估計能獲得![]() 萬元到
萬元到![]() 萬元的投資收益,討論了一個對課題組的獎勵方案:獎金
萬元的投資收益,討論了一個對課題組的獎勵方案:獎金![]() (單位:萬元)隨投資收益
(單位:萬元)隨投資收益![]() (單位:萬元)的增加而增加,且獎金不超過
(單位:萬元)的增加而增加,且獎金不超過![]() 萬元,同時獎金不超過投資收益的
萬元,同時獎金不超過投資收益的![]() .
.
(1)請分析函數![]() 是否符合華為要求的獎勵函數模型,并說明原因;
是否符合華為要求的獎勵函數模型,并說明原因;
(2)若華為公司采用模型函數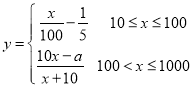 作為獎勵函數模型,試確定正整數
作為獎勵函數模型,試確定正整數![]() 的取值集合.
的取值集合.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com