
��֪�E�A ��a>b>0�����x���ʞ�
��a>b>0�����x���ʞ� ���ҽ��c(di��n)�飨
���ҽ��c(di��n)�飨 ��0����
��0����
��I����E�A�ķ��̣�
�����^�E�A���ҽ��c(di��n)��б�ʞ�k��ֱ���c�E�A�����c(di��n)A��xl��y1��,B��x2��y2������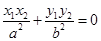 �� ��б��k�ǵ�ֵ��
�� ��б��k�ǵ�ֵ��
����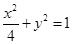 ����
����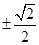
����ԇ�}�������������ҽ��c(di��n)��֪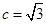 �����x���ʿ���
�����x���ʿ���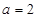 ������(j��)
������(j��)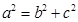 ����
����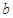 �������O(sh��)��ֱ������
�������O(sh��)��ֱ������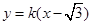 ��Ȼ��(li��n)��������y����x���õ��P(gu��n)��x��һԪ���η��̣��ٸ���(j��)�f�_(d��)�����ó����cϵ��(sh��)���P(gu��n)ϵʽ�������
��Ȼ��(li��n)��������y����x���õ��P(gu��n)��x��һԪ���η��̣��ٸ���(j��)�f�_(d��)�����ó����cϵ��(sh��)���P(gu��n)ϵʽ�������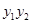 �ٌ�
�ٌ�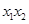 ��
��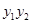 ����
����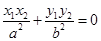 ���
��� ��ֵ��
��ֵ��
ԇ�}�������⣨����?y��n)��ҽ��c(di��n)�飨 ��0��������
��0��������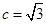 ����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/17/d/1pg5p2.png" style="vertical-align:middle;" />������
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/17/d/1pg5p2.png" style="vertical-align:middle;" />������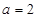 ��
��
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/b4/c/duukd2.png" style="vertical-align:middle;" />������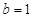
�ʙE�A���̞�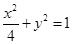 �� ����
�� ����
������?y��n)�ֱ��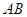 �^�ҽ��c(di��n)
�^�ҽ��c(di��n)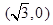 ���O(sh��)ֱ��
���O(sh��)ֱ��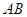 �ķ��̞�
�ķ��̞� 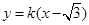 .
.
(li��n)�����̽M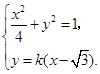
��ȥ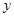 ��������
��������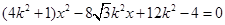 �� ��*��
�� ��*��
��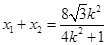 ��
�� ��
��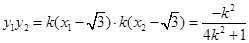 ��
��
��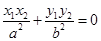 ����
����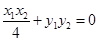 ��
��
����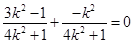 ���ɵ�
���ɵ� ����
����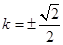 ��
��
���c(di��n)���E�A�Ļ��A(ch��)֪�R��ֱ���c�E�A��λ���P(gu��n)ϵ������������}����Q���}�Լ����w�c�D(zhu��n)��������������C�����|(zh��)��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪���タ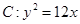 ���c(di��n)
���c(di��n)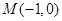 ���^
���^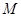 ��ֱ��
��ֱ�� �����タ
�����タ ��
�� ���c(di��n).
���c(di��n).
��1��������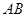 ���c(di��n)�ęM����(bi��o)����
���c(di��n)�ęM����(bi��o)����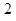 ����ֱ��
����ֱ�� ��б�ʣ�
��б�ʣ�
��2���O(sh��)�c(di��n)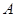 �P(gu��n)��
�P(gu��n)�� �S���Q�c(di��n)��
�S�Č��Q�c(di��n)��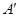 �����C��ֱ��
�����C��ֱ��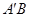 �^���c(di��n).
�^���c(di��n).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)�c(di��n)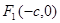 ��
��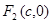 �քe�ǙE�A
�քe�ǙE�A �����ҽ��c(di��n),
�����ҽ��c(di��n),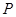 ��E�A
��E�A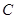 ������һ�c(di��n),��
������һ�c(di��n),��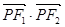 ����Сֵ��
����Сֵ�� .
.
��I����E�A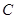 �ķ���;
�ķ���;
��II���O(sh��)ֱ��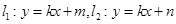 ��ֱ��
��ֱ��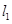 ��
��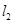 ���غϣ�,��
���غϣ�,��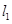 ��
��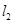 ���c�E�A
���c�E�A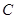 ���У�ԇ̽����
���У�ԇ̽����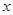 �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)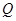 ,ʹ�c(di��n)
,ʹ�c(di��n)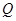 ��
��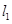 ��
��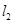 �ľ��x֮�e���1?������,Ո����c(di��n)
�ľ��x֮�e���1?������,Ո����c(di��n)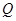 ����(bi��o);��������,Ո�f������.
����(bi��o);��������,Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D����֪�E�A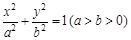 ������c(di��n)��A��2��0�����c(di��n)P��2e��
������c(di��n)��A��2��0�����c(di��n)P��2e��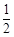 ���ڙE�A�ϣ�e��E�A���x���ʣ���
���ڙE�A�ϣ�e��E�A���x���ʣ���
��1����E�A�ķ��̣�
��2�����c(di��n)B��C��C�ڵ�һ���ޣ����ڙE�A�ϣ��M�� ����
���� ����(sh��)��(sh��)�˵�ֵ��
����(sh��)��(sh��)�˵�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵ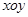 �У���֪
�У���֪ �քe�ǙE�A
�քe�ǙE�A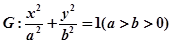 �����ҽ��c(di��n)���E�A
�����ҽ��c(di��n)���E�A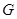 �c���タ
�c���タ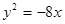 ��һ��(g��)�����Ľ��c(di��n)�����^�c(di��n)
��һ��(g��)�����Ľ��c(di��n)�����^�c(di��n)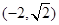 .
.
(��)��E�A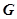 �ķ���;
�ķ���;
(��)�O(sh��)ֱ��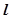 �c�E�A
�c�E�A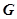 �ཻ��
�ཻ��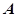 ��
��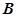 ���c(di��n),��
���c(di��n),��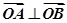 (
(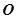 ������(bi��o)ԭ�c(di��n)),ԇ�Д�ֱ��
������(bi��o)ԭ�c(di��n)),ԇ�Д�ֱ��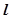 �c�A
�c�A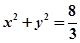 ��λ���P(gu��n)ϵ�����C����ĽY(ji��)Փ.
��λ���P(gu��n)ϵ�����C����ĽY(ji��)Փ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵ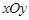 �У���֪�^�c(di��n)
�У���֪�^�c(di��n)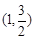 �ęE�A
�ęE�A ��
�� ���ҽ��c(di��n)��
���ҽ��c(di��n)��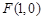 ���^���c(di��n)
���^���c(di��n)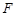 ���c
���c �S���غϵ�ֱ���c�E�A
�S���غϵ�ֱ���c�E�A ����
���� ��
�� ���c(di��n)���c(di��n)
���c(di��n)���c(di��n) �P(gu��n)������(bi��o)ԭ�c(di��n)�Č��Q�c(di��n)��
�P(gu��n)������(bi��o)ԭ�c(di��n)�Č��Q�c(di��n)�� ��ֱ��
��ֱ��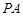 ��
��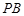 �քe���E�A
�քe���E�A ���Ҝ�(zh��n)��
���Ҝ�(zh��n)�� ��
��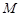 ��
��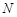 ���c(di��n).
���c(di��n).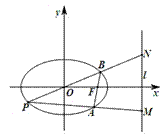
��1����E�A �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2�����c(di��n) ������(bi��o)��
������(bi��o)��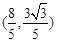 ��ԇ��ֱ��
��ԇ��ֱ��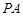 �ķ��̣�
�ķ��̣�
��3��ӛ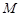 ��
��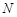 ���c(di��n)�Ŀv����(bi��o)�քe��
���c(di��n)�Ŀv����(bi��o)�քe��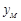 ��
��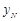 ��ԇ��
��ԇ��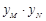 �Ƿ�鶨ֵ�����ǣ�Ո���ԓ��ֵ�������ǣ�Ո�f������.
�Ƿ�鶨ֵ�����ǣ�Ո���ԓ��ֵ�������ǣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D����֪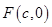 �ǙE�A
�ǙE�A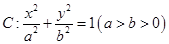 ���ҽ��c(di��n)���A
���ҽ��c(di��n)���A �c
�c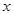 �S����
�S����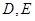 ���c(di��n)������
���c(di��n)������ �ǙE�A
�ǙE�A �����c(di��n).
�����c(di��n).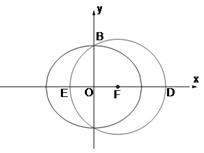
��1����E�A ���x���ʣ�
���x���ʣ�
��2���O(sh��)�A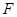 �c
�c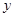 �S�������S�Ľ��c(di��n)��
�S�������S�Ľ��c(di��n)�� ���c(di��n)
���c(di��n) ���c(di��n)
���c(di��n) �P(gu��n)��
�P(gu��n)��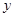 �S�Č��Q�c(di��n)��ԇ�Д�ֱ��
�S�Č��Q�c(di��n)��ԇ�Д�ֱ�� �c�A
�c�A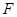 ��λ���P(gu��n)ϵ��
��λ���P(gu��n)ϵ��
��3���O(sh��)ֱ��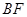 �c�A
�c�A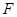 ������һ�c(di��n)
������һ�c(di��n) ����
����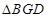 ����e��
����e��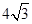 ����E�A
����E�A ��(bi��o)��(zh��n)����.
��(bi��o)��(zh��n)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A ��������ԭ�c(di��n)�����c(di��n)��
��������ԭ�c(di��n)�����c(di��n)�� �S�ϣ��ԃɂ�(g��)���c(di��n)�Ͷ��S�ăɂ�(g��)���c(di��n)����c(di��n)����߅����һ��(g��)��e��
�S�ϣ��ԃɂ�(g��)���c(di��n)�Ͷ��S�ăɂ�(g��)���c(di��n)����c(di��n)����߅����һ��(g��)��e��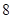 �������Σ�ӛ��
�������Σ�ӛ��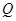 ��
��
������E�A �ķ���
�ķ���
�����O(sh��)�c(di��n) ��ֱ��
��ֱ��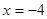 �c
�c �S�Ľ��c(di��n)���^�c(di��n)
�S�Ľ��c(di��n)���^�c(di��n) ��ֱ��
��ֱ�� �c�E�A
�c�E�A �ཻ��
�ཻ��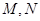 ���c(di��n)����(d��ng)����
���c(di��n)����(d��ng)����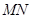 �����c(di��n)����������
�����c(di��n)����������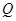 ��(n��i)������߅�磩�r(sh��)����ֱ��
��(n��i)������߅�磩�r(sh��)����ֱ�� б�ʵ�ȡֵ����
б�ʵ�ȡֵ����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�A�F����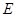 �ăɂ�(g��)���c(di��n)����(bi��o)��
�ăɂ�(g��)���c(di��n)����(bi��o)��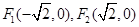 �����x���ʞ�
�����x���ʞ�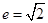 ��
��
����������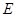 �ķ��̣�
�ķ��̣�
�����O(sh��)����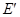 ��ʾ����
��ʾ����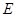 ��
��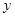 �S��߅���֣���ֱ��
�S��߅���֣���ֱ��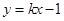 �c����
�c����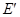 �ཻ��
�ཻ��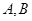 ���c(di��n)����
���c(di��n)����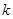 ��ȡֵ������
��ȡֵ������
�����ڗl�������£����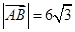 ��������
��������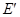 �ϴ����c(di��n)
�ϴ����c(di��n)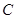 ��ʹ
��ʹ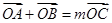 ����
����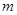 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com