
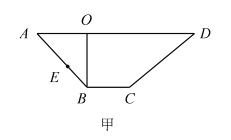
【題目】如圖甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,現將梯形
,現將梯形![]() 沿
沿![]() 折起如圖乙所示的四棱錐
折起如圖乙所示的四棱錐![]() ,使得
,使得![]() ,點
,點![]() 是線段
是線段![]() 上一動點.
上一動點.
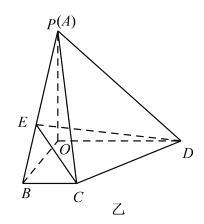
(1)證明: ![]() 和
和![]() 不可能垂直;
不可能垂直;
(2)當![]() 時,求
時,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)詳見解析; (2)![]() .
.
【解析】試題分析:由于折疊后![]() ,經過計算知
,經過計算知![]() ,這樣
,這樣![]() 兩兩垂直,因此以它們為坐標軸建立空間直角坐標系,寫出各點坐標.
兩兩垂直,因此以它們為坐標軸建立空間直角坐標系,寫出各點坐標.
(1)否定性命題,可假設![]() ,同時設
,同時設![]() (
(![]() ),利用向量垂直計算出
),利用向量垂直計算出![]() ,如果滿足
,如果滿足![]() 說明存在,如果不滿足
說明存在,如果不滿足![]() 說明不存在;
說明不存在;
(2)由![]() 得
得![]() 點坐標,從而可求出平面
點坐標,從而可求出平面![]() 的法向量
的法向量![]() ,則向量
,則向量![]() 與
與![]() 夾角的余弦的絕對值等于直線
夾角的余弦的絕對值等于直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
解析:如圖甲所示,因為![]() 是梯形
是梯形![]() 的高,
的高,![]() ,所以
,所以![]() ,因為
,因為![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,如圖乙所示,
,如圖乙所示,![]() ,
, ![]() ,
,![]() ,所以有
,所以有![]() ,所以
,所以![]() ,而
,而![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 、
、![]() 、
、![]() 兩兩垂直.故以
兩兩垂直.故以![]() 為原點,建立空間直角坐標系(如圖),則
為原點,建立空間直角坐標系(如圖),則![]() ,
,![]() ,
,![]() ,
,

(1)設![]() 其中
其中![]() ,所以
,所以![]() ,
,![]() ,假設
,假設![]() 和
和![]() 垂直,則
垂直,則![]() ,有
,有![]() ,解得
,解得![]() ,這與
,這與![]() 矛盾,假設不成立,所以
矛盾,假設不成立,所以![]() 和
和![]() 不可能垂直.
不可能垂直.
(2)因為![]() ,所以
,所以 ![]() ,設平面
,設平面![]() 的一個法向量是
的一個法向量是![]() ,因為
,因為![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,即
,即 ,取
,取![]() ,而
,而![]() ,所以
,所以 ,所以
,所以![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(x﹣ ![]() )cos(x﹣
)cos(x﹣ ![]() )(x∈R),則下面結論錯誤的是( )
)(x∈R),則下面結論錯誤的是( )
A.函數f(x)的圖象關于點(﹣ ![]() ,0)對稱
,0)對稱
B.函數f(x)的圖象關于直線x=﹣ ![]() 對稱
對稱
C.函數f(x)在區間[0, ![]() ]上是增函數
]上是增函數
D.函數f(x)的圖象是由函數y= ![]() sin2x的圖象向右平移
sin2x的圖象向右平移 ![]() 個單位而得到
個單位而得到
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費支出![]() (百萬元)與銷售額
(百萬元)與銷售額![]() (百萬元)之間有如下對應數據:
(百萬元)之間有如下對應數據:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果![]() 與
與![]() 之間具有線性相關關系.
之間具有線性相關關系.
(1)作出這些數據的散點圖;
(2)求這些數據的線性回歸方程![]() ;
;
(3)預測當廣告費支出為9百萬元時的銷售額。 ( 參考數據: ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m,n是兩條不同的直線,α、β是兩個不同的平面,則下列命題不正確的是________.
(1).若m⊥n,m⊥α,n![]() α,則n∥α
α,則n∥α
(2).若m⊥β,α⊥β,則m∥α或m![]() α
α
(3).若m⊥n,m⊥α,n⊥β,則α⊥β
(4).若![]() ∥α,α⊥β,則
∥α,α⊥β,則![]() ⊥β
⊥β
查看答案和解析>>
科目:高中數學 來源: 題型:
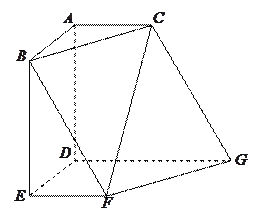
【題目】如圖,多面體![]() 中,
中, ![]() 兩兩垂直,平面
兩兩垂直,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.
(1)證明四邊形![]() 是正方形;
是正方形;
(2)判斷點![]() 是否四點共面,并說明為什么?
是否四點共面,并說明為什么?
(3)連結![]() ,求證:
,求證: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設某種設備使用的年限x(年)與所支出的維修費用y(萬元)有以下統計資料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
維修費用y | 2 | 4 | 5 | 6 | 7 |
若由資料知y對x呈線性相關關系。試求:
(1)求![]() ; (2)線性回歸方程
; (2)線性回歸方程![]() ;
;
(3)估計使用10年時,維修費用是多少?
附:利用“最小二乘法”計算a,b的值時,可根據以下公式:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點M是棱長為2的正方體的棱AD的中點,P是平面![]() 內一點,若面
內一點,若面![]() 分別與面ABCD和面
分別與面ABCD和面![]() 所成的銳二面角相等,則
所成的銳二面角相等,則![]() 長度的最小值是( )
長度的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com