Question

觀察下列算式：
1²=1
2²=1+3
3²=1+3+5
4²=1+3+5+7
…
若某個n²按上述規律展開后，等式右邊含有2013，則n的最小值為    ．

Answer 1

【答案】分析：觀察算式可得規律：第n行的左邊是n²，右邊是n個連續奇數的和．若某個n²按上述規律展開后，等式右邊含有2013，即第n行的第一個數為1，最后一個數是2013，累加可得n²，即由n²=1+3+…+2013計算可得．
解答：解：由題意可得第n行的左邊是n²，右邊是n個連續奇數的和，
若某個n²按上述規律展開后，等式右邊含有2013，
即第n行的第一個數為1，最后一個數是2013，累加可得n²，
即n²=1+3+…+2013，
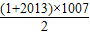
由于1+3+…+2013==1007²，可得n=1007．
故答案為：1007．
點評：本題考查歸納推理，涉及等差數列的求和問題，屬基礎題．