
【題目】已知圓C的圓心在直線l:y=2x上,且經過點A(﹣3,﹣1),B(4,6).
(Ⅰ)求圓C的方程;
(Ⅱ)點P是直線l上橫坐標為﹣4的點,過點P作圓C的切線,求切線方程.
 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函數f(x)的定義域;
(2)若函數f(x)的最小值為﹣4,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)滿足f(0)=2和f(x+1)﹣f(x)=2x﹣1對任意實數x都成立.
(1)求函數f(x)的解析式;
(2)當t∈[﹣1,3]時,求y=f(2t)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
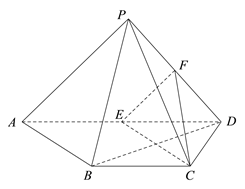
【題目】如圖,四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為
線段![]() ,
, ![]() 的中點.
的中點.
(Ⅰ)求證: ![]() //平面
//平面![]() ;
;
(Ⅱ)求證: ![]() 平面
平面![]() ;
;
(Ⅲ)寫出三棱錐![]() 與三棱錐
與三棱錐![]() 的體積之比.(結論不要求證明)
的體積之比.(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+2ax+2,x∈[﹣5,5].
(1)求實數a的范圍,使y=f(x)在區間[﹣5,5]上是單調函數.
(2)求f(x)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=log ![]()
![]() 為奇函數,a為常數,
為奇函數,a為常數,
(1)求a的值;
(2)證明f(x)在區間(1,+∞)上單調遞增;
(3)若x∈[3,4],不等式f(x)>( ![]() )x+m恒成立,求實數m的取值范圍.
)x+m恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某社區超市購進了A,B,C,D四種新產品,為了解新產品的銷售情況,該超市隨機調查了15位顧客(記為![]() )購買這四種新產品的情況,記錄如下(單位:件):
)購買這四種新產品的情況,記錄如下(單位:件):
顧 客 產 品 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A | 1 | 1 | 1 | 1 | 1 | ||||||||||
B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
D | 1 | 1 | 1 | 1 | 1 | 1 |
(Ⅰ)若該超市每天的客流量約為300人次,一個月按30天計算,試估計產品A的月銷售量(單位:件);
(Ⅱ)為推廣新產品,超市向購買兩種以上(含兩種)新產品的顧客贈送2元電子紅包.現有甲、乙、丙三人在該超市購物,記他們獲得的電子紅包的總金額為X,
求隨機變量X的分布列和數學期望;
(Ⅲ)若某顧客已選中產品B,為提高超市銷售業績,應該向其推薦哪種新產品?(結果不需要證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分12分)為選拔選手參加“中國漢字聽寫大會”,某中學舉行了一次“漢字聽寫大賽”活動.為了了解本次競賽學生的成績情況,從中抽取了部分學生的分數(得分取正整數,滿分為100分)作為樣本(樣本容量為![]() )進行統計.按照
)進行統計.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(圖中僅列出了得分在
的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(圖中僅列出了得分在![]() ,
, ![]() 的數據).
的數據).

(1)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 、
、![]() 的值;
的值;
(2)在選取的樣本中,從競賽成績在80分以上(含80分)的學生中隨機抽取2名學生參加“中國漢字聽寫大會”,求所抽取的2名學生中至少有一人得分在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() ,離心率
,離心率![]() ,它的長軸長等于圓
,它的長軸長等于圓![]() 的直徑.
的直徑.
(1)求橢圓 ![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,是否存在定點
兩點,是否存在定點![]() ,使得以
,使得以![]() 為直徑的圓經過這個定點,若存在,求出定點
為直徑的圓經過這個定點,若存在,求出定點![]() 的坐標;若不存在,請說明理由?
的坐標;若不存在,請說明理由?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com