
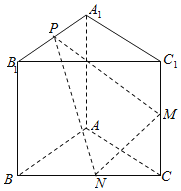
【題目】如圖,已知三棱柱![]() 的側棱與底面垂直,
的側棱與底面垂直,![]() ,
,![]() ,M是
,M是![]() 的中點,
的中點,![]() 是
是![]() 的中點,點
的中點,點![]() 在
在![]() 上,且滿足
上,且滿足![]() .
.
(1)證明:![]() .
.
(2)當![]() 取何值時,直線
取何值時,直線![]() 與平面
與平面![]() 所成的角
所成的角![]() 最大?并求該角最大值的正切值.
最大?并求該角最大值的正切值.
(3)若平面![]() 與平面
與平面![]() 所成的二面角為
所成的二面角為![]() ,試確定P點的位置.
,試確定P點的位置.
【答案】(1)見解析;(2)見解析;(3)見解析
【解析】
(1)以AB,AC,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() ,求出各點的坐標及對應向量的坐標,易判斷
,求出各點的坐標及對應向量的坐標,易判斷![]() ,即
,即![]() ;(2)設出平面ABC的一個法向量,我們易表達出
;(2)設出平面ABC的一個法向量,我們易表達出![]() ,然后利用正弦函數的單調性及正切函數的單調性的關系,求出滿足條件的
,然后利用正弦函數的單調性及正切函數的單調性的關系,求出滿足條件的![]() 值,進而求出此時
值,進而求出此時![]() 的正線值;(3)平面PMN與平面ABC所成的二面角為
的正線值;(3)平面PMN與平面ABC所成的二面角為![]() ,則平面PMN與平面ABC法向量的夾角余弦值的絕對值為
,則平面PMN與平面ABC法向量的夾角余弦值的絕對值為![]() ,代入向量夾角公式,可以構造一個關于
,代入向量夾角公式,可以構造一個關于![]() 的方程,解方程即可求出對應
的方程,解方程即可求出對應![]() 值,進而確定出滿足條件的點P的位置.
值,進而確定出滿足條件的點P的位置.
(1)證明:如圖,以AB,AC,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() .
.
則![]() ,
,![]() ,
,![]() ,
,
從而![]() ,
,![]() ,
,
![]() ,
,
所以![]() .
.
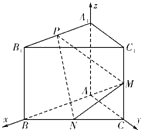
(2)平面ABC的一個法向量為![]() ,
,
則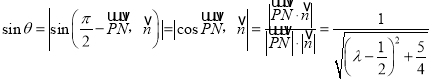 (※).
(※).
而![]() ,當
,當![]() 最大時,
最大時,![]() 最大,
最大,![]() 無意義,
無意義,![]() 除外,
除外,
由(※)式,當![]() 時,
時,![]() ,
,![]() .
.
(3)平面ABC的一個法向量為![]() .
.
設平面PMN的一個法向量為![]() ,
,
由(1)得![]() .
.
由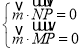 得
得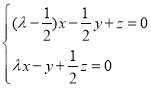 ,
,
解得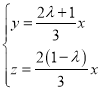 ,令
,令![]() ,得
,得![]() ,
,
∵平面PMN與平面ABC所成的二面角為![]() ,
,
∴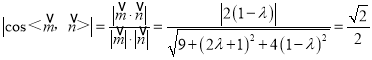 ,
,
解得![]() .
.
故點P在![]() 的延長線上,且
的延長線上,且![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的長軸長為4,焦距為
的長軸長為4,焦距為![]()
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過動點![]() 的直線交
的直線交![]() 軸與點
軸與點![]() ,交
,交![]() 于點
于點![]() (
(![]() 在第一象限),且
在第一象限),且![]() 是線段
是線段![]() 的中點.過點
的中點.過點![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 于另一點
于另一點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() .
.
(ⅰ)設直線![]() 的斜率分別為
的斜率分別為![]() ,證明
,證明![]() 為定值;
為定值;
(ⅱ)求直線![]() 的斜率的最小值.
的斜率的最小值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果你留心使會發現,汽車前燈后的反射鏡呈拋物線的形狀,把拋物線沿它的對稱軸旋轉一周,就會形成一個拋物面.這種拋物面形狀,正是我們熟悉的汽車前燈的反射鏡形狀,這種形狀使車燈既能夠發出明亮的、照射很遠的平行光束,又能發出較暗的,照射近距離的光線.我們都知道常規的前照燈主要是由燈泡、反射鏡和透鏡三部分組成,明亮的光束,是由位于拋物面形狀反射鏡焦點的光源射出的,燈泡位于拋物面的焦點上,燈泡發出的光經拋物面反射鏡反射形成平行光束,再經過配光鏡的散射、偏轉作用,以達到照亮路面的效果,這樣的燈光我們通常稱為遠光燈:而較暗的光線,不是由反射鏡焦點的光源射出的,光線的行進與拋物線的對稱軸不平行,光線只能向上和向下照射,所以照射距離并不遠,如果把向上射出的光線遮住.車燈就只能發出向下的、射的很近的光線了.請用數學的語言歸納表達遠光燈的照明原理,并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了選拔學生參加全市中學生物理競賽,學校先從高三年級選取60名同學進行競賽預選賽,將參加預選賽的學生成績(單位:分)按范圍![]() ,
,![]() ,
,![]() ,
,![]() 分組,得到的頻率分布直方圖如圖:
分組,得到的頻率分布直方圖如圖:

(1)計算這次預選賽的平均成績(同一組中的數據用該組區間的中點值作代表);
(2)若對得分在前![]() 的學生進行校內獎勵,估計獲獎分數線;
的學生進行校內獎勵,估計獲獎分數線;
(3)若這60名學生中男女生比例為![]() ,成績不低于60分評估為“成績良好”,否則評估為“成績一般”,試完成下面
,成績不低于60分評估為“成績良好”,否則評估為“成績一般”,試完成下面![]() 列聯表,是否有
列聯表,是否有![]() 的把握認為“成績良好”與“性別”有關?
的把握認為“成績良好”與“性別”有關?
成績良好 | 成績一般 | 合計 | |
男生 | |||
女生 | |||
合計 |
附:![]() ,
,![]()
臨界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() ,圓
,圓![]() :
:![]() .
.
(1)若過拋物線![]() 的焦點
的焦點![]() 的直線
的直線![]() 與圓
與圓![]() 相切,求直線
相切,求直線![]() 方程;
方程;
(2)在(1)的條件下,若直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 軸上是否存在點
軸上是否存在點![]() 使
使![]() (
(![]() 為坐標原點)?若存在,求出點
為坐標原點)?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《九章算術》中記載了有關特殊幾何體的定義:陽馬指底面為矩形,一側棱垂直于底面的四棱錐,塹堵指底面是直角三角形,且側棱垂直于底面的三棱柱.
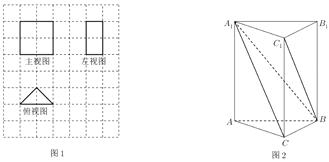
(1)某塹堵的三視圖,如圖1,網格中的每個小正方形的邊長為1,求該塹堵的體積;
(2)在塹堵![]() 中,如圖2,
中,如圖2,![]() ,若
,若![]() ,當陽馬
,當陽馬![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某人打算做一個正四棱錐形的金字塔模型,先用木料搭邊框,再用其他材料填充,已知金字塔的每一條棱和邊都相等.
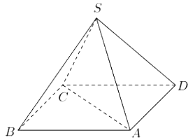
(1)求證:直線AC垂直于直線SD;
(2)若搭邊框共使用木料24米,則需要多少立方米的填充材料才能將整個金字塔內部填滿?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知無窮數列![]() 的各項都不為零,其前n項和為
的各項都不為零,其前n項和為![]() ,且滿足
,且滿足![]() ,數列
,數列![]() 滿足
滿足![]() ,其中t為正整數.
,其中t為正整數.
![]() 求
求![]() ;
;
![]() 若不等式
若不等式![]() 對任意
對任意![]() 都成立,求首項
都成立,求首項![]() 的取值范圍;
的取值范圍;
![]() 若首項
若首項![]() 是正整數,則數列
是正整數,則數列![]() 中的任意一項是否總可以表示為數列
中的任意一項是否總可以表示為數列![]() 中的其他兩項之積?若是,請給出一種表示方式;若不是,請說明理由.
中的其他兩項之積?若是,請給出一種表示方式;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com