
(本小題12分)某公司生產(chǎn)一種產(chǎn)品每年需投入固定成本為0.5萬元,此外每生產(chǎn)100件這種產(chǎn)品還需要增加投入0.25萬元.經(jīng)預(yù)測知,當(dāng)售出這種產(chǎn)品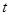 百件時,若
百件時,若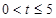 ,則銷售所得的收入為
,則銷售所得的收入為 萬元:若
萬元:若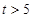 ,則銷售收入為
,則銷售收入為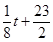 萬元.
萬元.
(1)若該公司的這種產(chǎn)品的年產(chǎn)量為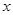 百件
百件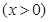 ,請把該公司生產(chǎn)并銷售這種產(chǎn)品所得的年利潤
,請把該公司生產(chǎn)并銷售這種產(chǎn)品所得的年利潤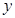 表示為當(dāng)年生產(chǎn)量
表示為當(dāng)年生產(chǎn)量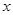 的函數(shù);
的函數(shù);
(2)當(dāng)年產(chǎn)量為多少時,當(dāng)年公司所獲利潤最大?
(1)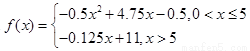
(2)當(dāng)年產(chǎn)量為4.75(百件)時,當(dāng)年公司所得利潤最大,最大為10.78125萬元.
【解析】
試題分析:(1)分類討論:①當(dāng)0≤x≤5時,②當(dāng)x>5時,分別寫出函數(shù)f(x)的表達(dá)式,最后利用分段函數(shù)的形式寫出所求函數(shù)解析式即可;
(2)分別求出當(dāng)0≤x≤5時,及當(dāng)x>5時,f(x)的最大值,最后綜上所述,當(dāng)x為多少時,f(x)有最大值,即當(dāng)年產(chǎn)量為多少件時,公司可獲得最大年利潤.
解:(1)當(dāng)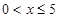 時,
時,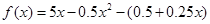 =
=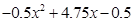
當(dāng)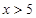 時,
時,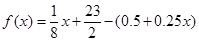

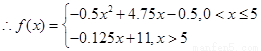
(2)當(dāng)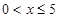 時,
時,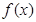 =
=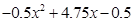 =
=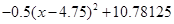
 當(dāng)
當(dāng)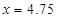 時,
時,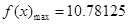
當(dāng)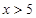 時,
時,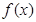

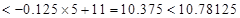
 當(dāng)年產(chǎn)量為4.75(百件)時,當(dāng)年公司所得利潤最大,最大為10.78125萬元.
當(dāng)年產(chǎn)量為4.75(百件)時,當(dāng)年公司所得利潤最大,最大為10.78125萬元.
考點(diǎn):本題主要考查了分段函數(shù),以及函數(shù)與方程的思想,屬于基礎(chǔ)題..
點(diǎn)評:解決該試題的關(guān)鍵是函數(shù)模型為分段函數(shù),求分段函數(shù)的最值,應(yīng)先求出函數(shù)在各部分的最值,然后取各部分的最值的最大值為整個函數(shù)的最大值,取各部分的最小者為整個函數(shù)的最小值。



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com