
分析 (Ⅰ)由題意列關于a,b,c的方程組,求解得到a,b的值,則橢圓方程可求;
(Ⅱ)求出PA,PB,證明|PA|≠|PB|,即可證明:△PAB不可能為等邊三角形.
解答 (I)解:由題意,得$\left\{\begin{array}{l}{\frac{9}{4{a}^{2}}+\frac{6}{4{b}^{2}}=1}\\{\frac{c}{a}=\frac{\sqrt{3}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得${a}^{2}=\frac{9}{2},{b}^{2}=3$.
∴橢圓C的標準方程為$\frac{2{x}^{2}}{9}+\frac{{y}^{2}}{3}=1$;
(II)證明:證明:A(x1,y1),則$2{{x}_{1}}^{2}+3{{y}_{1}}^{2}=9$,且x1∈[-$\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$],
|PA|=$\sqrt{({x}_{1}-1)^{2}+{y}_{1}2}$=$\sqrt{({x}_{1}-1)^{2}+3-\frac{2}{3}{{x}_{1}}^{2}}$=$\sqrt{\frac{1}{3}({x}_{1}-3)^{2}+1}$,
B(x2,y2),同理可得|PB|=$\sqrt{\frac{1}{3}({x}_{2}-3)^{2}+1}$,且x2∈[-$\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$].
y=$\frac{1}{3}(x-3)^{2}+1$在[-$\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$]上單調,
∴有x1=x2?|PA|=|PB|,
∵x1≠x2,∴|PA|≠|PB|,
∴△PAB不可能為等邊三角形.
點評 本題考查直線與橢圓的位置關系,考查兩點間距離公式的運用,考查學生的計算能力,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | 當x<0,有極大值為2-$\frac{4}{e}$ | B. | 當x<0,有極小值為2-$\frac{4}{e}$ | ||
| C. | 當x>0,有極大值為0 | D. | 當x>0,有極小值為0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y2=±2$\sqrt{2}$x | B. | y2=±2x | C. | y2=±4x | D. | y2=±4$\sqrt{2}$x |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
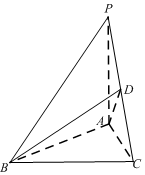 如圖,在底面是正三角形的三棱錐P-ABC中,D為PC的中點,PA=AB=1,PB=PC=$\sqrt{2}$.
如圖,在底面是正三角形的三棱錐P-ABC中,D為PC的中點,PA=AB=1,PB=PC=$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{10}{17}$ | B. | $\frac{14}{17}$ | C. | $\frac{9}{16}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com