
(本小題滿分14分)
已知函數f(x)=(x2+ax-2a-3)·e3-x (a∈R)
(1)討論f(x)的單調性;
(2)設g(x)=(a2+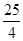 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范圍.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范圍.
⑴ ,此時
,此時 在
在 上為減函數,在
上為減函數,在 上為增函數,在
上為增函數,在 上為減函數;
上為減函數;
當 時,
時, ,此時
,此時 在
在 上為減函數;
上為減函數;
當 時,此時
時,此時 在
在 上為減函數,在
上為減函數,在 上為增函數,在
上為增函數,在 上為減函數.
上為減函數.
⑵ a的取值范圍為 .
.
解析試題分析:⑴ ,令
,令 ,
,
即 所以
所以
所以 …………………………………………………………………3分
…………………………………………………………………3分 ,此時
,此時 在
在 上為減函數,在
上為減函數,在 上為增函數,在
上為增函數,在 上為減函數;
上為減函數;
當 時,
時, ,此時
,此時 在
在 上為減函數;
上為減函數;
當 時,此時
時,此時 在
在 上為減函數,在
上為減函數,在 上為增函數,在
上為增函數,在 上為減函數. ………………………………………………………………………………6分
上為減函數. ………………………………………………………………………………6分
⑵ 當 時,
時, ,則
,則 在
在 上為增函數,在
上為增函數,在 上為減函數
上為減函數
又
∴ 在
在 上的值域為
上的值域為 ………………………………………8分
………………………………………8分
又 在
在 上為增函數,其值域為
上為增函數,其值域為 ……10分
……10分
 等價于
等價于 ……………………………………………12分
……………………………………………12分 存在
存在 使得
使得 成立,只須
成立,只須
 ,又
,又
∴a的取值范圍為 . ………………………………………………………………14分
. ………………………………………………………………14分
考點:本題主要考查應用導數研究函數的單調性,恒成立問題。
點評:典型題,本題屬于導數應用中的基本問題,(2)涉及恒成立問題,轉化成求函數的最值,這種思路是一般解法,往往要利用“分離參數法”,本題最終化為最值之間故選的研究,體現考題“起點高,落點低”的特點。


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分14分)已知函數 。
。
(Ⅰ)若函數 在定義域內為增函數,求實數
在定義域內為增函數,求實數 的取值范圍;
的取值范圍;
(Ⅱ)設 ,若函數
,若函數 存在兩個零點
存在兩個零點 ,且滿足
,且滿足 ,問:函數
,問:函數 在
在 處的切線能否平行于
處的切線能否平行于 軸?若能,求出該切線方程;若不能,請說明理由。
軸?若能,求出該切線方程;若不能,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數
(1)若函數y=f(x)的圖象切x軸于點(2,0),求a、b的值;
(2)設函數y="f(x)"  的圖象上任意一點的切線斜率為k,試求
的圖象上任意一點的切線斜率為k,試求 的充要條件;(3)若函數y=f(x)的圖象上任意不同的兩點的連線的斜率小于1,求證
的充要條件;(3)若函數y=f(x)的圖象上任意不同的兩點的連線的斜率小于1,求證 。
。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com