
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過(guò)橢圓E的左焦點(diǎn)
,過(guò)橢圓E的左焦點(diǎn)![]() 且與x軸垂直的直線與橢圓E相交于的P,Q兩點(diǎn),O為坐標(biāo)原點(diǎn),
且與x軸垂直的直線與橢圓E相交于的P,Q兩點(diǎn),O為坐標(biāo)原點(diǎn),![]() 的面積為
的面積為![]() .
.
(1)求橢圓E的方程;
(2)點(diǎn)M,N為橢圓E上不同兩點(diǎn),若![]() ,求證:
,求證:![]() 的面積為定值.
的面積為定值.
【答案】(1) ![]() (2)證明見(jiàn)解析
(2)證明見(jiàn)解析
【解析】
(1)離心率提供一個(gè)等式![]() ,
,![]() 是橢圓的通徑,通徑長(zhǎng)為
是橢圓的通徑,通徑長(zhǎng)為![]() ,這樣
,這樣![]() 的面積又提供一個(gè)等式
的面積又提供一個(gè)等式![]() ,兩者聯(lián)立方程組結(jié)合
,兩者聯(lián)立方程組結(jié)合![]() ,可求得
,可求得![]() 得橢圓標(biāo)準(zhǔn)方程.
得橢圓標(biāo)準(zhǔn)方程.
(2)設(shè)![]() ,由
,由![]() 得
得![]() ,當(dāng)直線
,當(dāng)直線![]() 的斜率存在時(shí),設(shè)直線
的斜率存在時(shí),設(shè)直線![]() 的方程為
的方程為![]() ,代入橢圓方程并整理,得
,代入橢圓方程并整理,得![]() .應(yīng)用韋達(dá)定理得
.應(yīng)用韋達(dá)定理得![]() ,代入
,代入 ![]() 可得
可得![]() 的關(guān)系,注意
的關(guān)系,注意![]() ,然后由圓錐曲線中的弦長(zhǎng)公式計(jì)算弦長(zhǎng)
,然后由圓錐曲線中的弦長(zhǎng)公式計(jì)算弦長(zhǎng)![]() ,求出
,求出![]() 到直線
到直線![]() 的距離,求得
的距離,求得![]() 的面積,化簡(jiǎn)可得為定值,同樣直線
的面積,化簡(jiǎn)可得為定值,同樣直線![]() 的不斜率存在時(shí),也求得
的不斜率存在時(shí),也求得![]() 的面積和剛才一樣,即得結(jié)論.
的面積和剛才一樣,即得結(jié)論.
(1)設(shè)橢圓的半焦距為c,則![]() ①
①
過(guò)橢圓左焦點(diǎn)![]() 且與x軸垂直的直線方程為
且與x軸垂直的直線方程為![]() ,與橢圓方程聯(lián)立解得
,與橢圓方程聯(lián)立解得![]() ,
,
所以![]() ,所以
,所以![]() ②
②
把①代入②,解得![]()
又![]() ,解得
,解得![]()
所以E的方程為:![]()
(2)設(shè)![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,
,
即![]()
(i)當(dāng)直線![]() 的斜率存在時(shí),設(shè)直線
的斜率存在時(shí),設(shè)直線![]() 的方程為
的方程為![]() ,代入橢圓方程并整理,得
,代入橢圓方程并整理,得![]() .
.
則![]() ,
,![]()
![]() ③
③
![]()
所以![]() ,整理得
,整理得![]() ,代入③,
,代入③,![]()
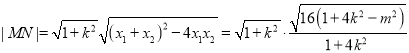 ,
,
O到直線![]() 的距離
的距離![]() ,
,
所以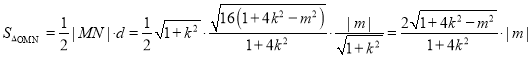
![]() ,即
,即![]() 的面積為定值1
的面積為定值1
(ii)當(dāng)直線![]() 的斜率不存在時(shí),不妨設(shè)
的斜率不存在時(shí),不妨設(shè)![]() 的斜率為
的斜率為![]() 且點(diǎn)M在第一象限,此時(shí)
且點(diǎn)M在第一象限,此時(shí)![]() 的方程為
的方程為![]() ,代入橢圓方程,解得
,代入橢圓方程,解得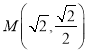 ,此時(shí)
,此時(shí)![]() 的面積為
的面積為 .
.
綜上可知,![]() 的面積為定值1
的面積為定值1


 各地期末復(fù)習(xí)特訓(xùn)卷系列答案
各地期末復(fù)習(xí)特訓(xùn)卷系列答案 小博士期末闖關(guān)100分系列答案
小博士期末闖關(guān)100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)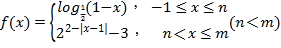 的值域是
的值域是![]() ,有下列結(jié)論:①當(dāng)
,有下列結(jié)論:①當(dāng)![]() 時(shí),
時(shí),![]() ; ②當(dāng)
; ②當(dāng)![]() 時(shí),
時(shí),![]() ;③當(dāng)
;③當(dāng)![]() 時(shí),
時(shí),![]() ; ④當(dāng)
; ④當(dāng)![]() 時(shí),
時(shí),![]() .其中結(jié)論正確的所有的序號(hào)是( ).
.其中結(jié)論正確的所有的序號(hào)是( ).
A.①②B.③④C.②③D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在邊長(zhǎng)為![]() 的等邊三角形
的等邊三角形![]() 中,點(diǎn)
中,點(diǎn)![]() 分別是邊
分別是邊![]() 上的點(diǎn),滿足
上的點(diǎn),滿足![]() 且
且![]()
![]() ,將
,將![]() 沿直線
沿直線![]() 折到
折到![]() 的位置. 在翻折過(guò)程中,下列結(jié)論成立的是( )
的位置. 在翻折過(guò)程中,下列結(jié)論成立的是( )
A.在邊![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使得在翻折過(guò)程中,滿足
,使得在翻折過(guò)程中,滿足![]() 平面
平面![]()
B.存在![]() ,使得在翻折過(guò)程中的某個(gè)位置,滿足平面
,使得在翻折過(guò)程中的某個(gè)位置,滿足平面![]() 平面
平面![]()
C.若![]() ,當(dāng)二面角
,當(dāng)二面角![]() 為直二面角時(shí),
為直二面角時(shí),![]()
D.在翻折過(guò)程中,四棱錐![]() 體積的最大值記為
體積的最大值記為![]() ,
,![]() 的最大值為
的最大值為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() ,其中
,其中![]() 為正實(shí)數(shù).
為正實(shí)數(shù).
(1)若不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時(shí),證明
時(shí),證明![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系上,有一點(diǎn)列![]() ,設(shè)點(diǎn)
,設(shè)點(diǎn)![]() 的坐標(biāo)
的坐標(biāo)![]() (
(![]() ),其中
),其中![]() . 記
. 記![]() ,
,![]() ,且滿足
,且滿足![]() (
(![]() ).
).
(1)已知點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 滿足
滿足![]() ,求
,求![]() 的坐標(biāo);
的坐標(biāo);
(2)已知點(diǎn)![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是遞增數(shù)列,點(diǎn)
)是遞增數(shù)列,點(diǎn)![]() 在直線
在直線![]() :
:![]() 上,求
上,求![]() ;
;
(3)若點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】分形幾何學(xué)是數(shù)學(xué)家伯努瓦曼德?tīng)柌剂_在20世紀(jì)70年代創(chuàng)立的一門新的數(shù)學(xué)學(xué)科.它的創(chuàng)立為解決傳統(tǒng)科學(xué)眾多領(lǐng)域的難題提供了全新的思路.按照如圖1所示的分形規(guī)律可得如圖2所示的一個(gè)樹形圖:
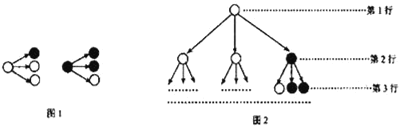
易知第三行有白圈5個(gè),黑圈4個(gè).我們采用“坐標(biāo)”來(lái)表示各行中的白圈、黑圈的個(gè)數(shù).比如第一行記為![]() ,第二行記為
,第二行記為![]() ,第三行記為
,第三行記為![]() .照此規(guī)律,第
.照此規(guī)律,第![]() 行中的白圈、黑圈的“坐標(biāo)”為
行中的白圈、黑圈的“坐標(biāo)”為![]() ,則
,則![]() ________.
________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,點(diǎn)A為該橢圓的左頂點(diǎn),過(guò)右焦點(diǎn)
,點(diǎn)A為該橢圓的左頂點(diǎn),過(guò)右焦點(diǎn)![]() 的直線l與橢圓交于B,C兩點(diǎn),當(dāng)
的直線l與橢圓交于B,C兩點(diǎn),當(dāng)![]() 軸時(shí),三角形ABC的面積為18.
軸時(shí),三角形ABC的面積為18.
![]() 求橢圓
求橢圓![]() 的方程;
的方程;
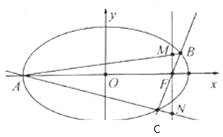
![]() 如圖,當(dāng)動(dòng)直線BC斜率存在且不為0時(shí),直線
如圖,當(dāng)動(dòng)直線BC斜率存在且不為0時(shí),直線![]() 分別交直線AB,AC于點(diǎn)M、N,問(wèn)x軸上是否存在點(diǎn)P,使得
分別交直線AB,AC于點(diǎn)M、N,問(wèn)x軸上是否存在點(diǎn)P,使得![]() ,若存在求出點(diǎn)P的坐標(biāo);若不存在說(shuō)明理由.
,若存在求出點(diǎn)P的坐標(biāo);若不存在說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
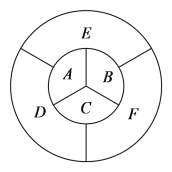
【題目】如下圖中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六個(gè)區(qū)域進(jìn)行染色,每個(gè)區(qū)域只染一種顏色,每個(gè)區(qū)域只染一種顏色,且相鄰的區(qū)域不同色.若有
六個(gè)區(qū)域進(jìn)行染色,每個(gè)區(qū)域只染一種顏色,每個(gè)區(qū)域只染一種顏色,且相鄰的區(qū)域不同色.若有![]() 種顏色可供選擇,則共有_________種不同的染色方案.
種顏色可供選擇,則共有_________種不同的染色方案.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】有一矩形硬紙板材料(厚度忽略不計(jì)),一邊![]() 長(zhǎng)為6分米,另一邊足夠長(zhǎng).現(xiàn)從中截取矩形
長(zhǎng)為6分米,另一邊足夠長(zhǎng).現(xiàn)從中截取矩形![]() (如圖甲所示),再剪去圖中陰影部分,用剩下的部分恰好能折卷成一個(gè)底面是弓形的柱體包裝盒(如圖乙所示,重疊部分忽略不計(jì)),其中
(如圖甲所示),再剪去圖中陰影部分,用剩下的部分恰好能折卷成一個(gè)底面是弓形的柱體包裝盒(如圖乙所示,重疊部分忽略不計(jì)),其中![]() 是以
是以![]() 為圓心、
為圓心、![]() 的扇形,且弧
的扇形,且弧![]() ,
,![]() 分別與邊
分別與邊![]() ,
, ![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,
, ![]() .
.
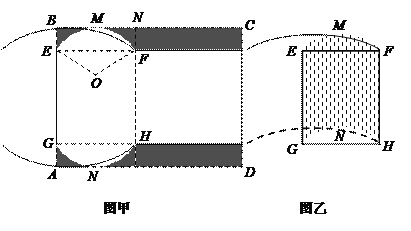
(1)當(dāng)![]() 長(zhǎng)為1分米時(shí),求折卷成的包裝盒的容積;
長(zhǎng)為1分米時(shí),求折卷成的包裝盒的容積;
(2)當(dāng)![]() 的長(zhǎng)是多少分米時(shí),折卷成的包裝盒的容積最大?
的長(zhǎng)是多少分米時(shí),折卷成的包裝盒的容積最大?
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com