
【題目】已知函數(shù)![]() ,其中無理數(shù)
,其中無理數(shù)![]() .
.
(Ⅰ)若函數(shù)![]() 有兩個(gè)極值點(diǎn),求
有兩個(gè)極值點(diǎn),求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若函數(shù)![]() 的極值點(diǎn)有三個(gè),最小的記為
的極值點(diǎn)有三個(gè),最小的記為![]() ,最大的記為
,最大的記為![]() ,若
,若![]() 的最大值為
的最大值為![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)先對(duì)函數(shù)![]() 求導(dǎo),構(gòu)造
求導(dǎo),構(gòu)造![]() ,則函數(shù)
,則函數(shù)![]() 有兩個(gè)極值點(diǎn)等價(jià)于
有兩個(gè)極值點(diǎn)等價(jià)于![]()
![]() 有兩個(gè)不等的正實(shí)根,對(duì)函數(shù)
有兩個(gè)不等的正實(shí)根,對(duì)函數(shù)![]() 求導(dǎo),然后對(duì)
求導(dǎo),然后對(duì)![]() 和
和![]() 進(jìn)行討論,可得函數(shù)
進(jìn)行討論,可得函數(shù)![]() 的單調(diào)性,結(jié)合
的單調(diào)性,結(jié)合![]() ,即可求得
,即可求得![]() 的取值范圍;(Ⅱ)對(duì)函數(shù)
的取值范圍;(Ⅱ)對(duì)函數(shù)![]() 求導(dǎo),由
求導(dǎo),由![]() 有三個(gè)極值點(diǎn),則
有三個(gè)極值點(diǎn),則![]() 有三個(gè)零點(diǎn),1為一個(gè)零點(diǎn),其他兩個(gè)則為
有三個(gè)零點(diǎn),1為一個(gè)零點(diǎn),其他兩個(gè)則為![]() 的零點(diǎn),結(jié)合(Ⅰ),可得
的零點(diǎn),結(jié)合(Ⅰ),可得![]() 的兩個(gè)零點(diǎn)即為
的兩個(gè)零點(diǎn)即為![]() 的最小和最大極值點(diǎn)
的最小和最大極值點(diǎn)![]() ,
,![]() ,即
,即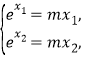 ,令
,令![]() ,由題知
,由題知![]() ,則
,則![]() ,令
,令![]() ,利用導(dǎo)數(shù)研究函數(shù)
,利用導(dǎo)數(shù)研究函數(shù)![]() 的單調(diào)性,從而可求得
的單調(diào)性,從而可求得![]() 的最小值即
的最小值即![]() 的最小值.
的最小值.
詳解:(Ⅰ)![]() ,
,
令![]() ,
,![]() ,
,
∵![]() 有兩個(gè)極值點(diǎn)
有兩個(gè)極值點(diǎn)
∴![]()
![]() 有兩個(gè)不等的正實(shí)根
有兩個(gè)不等的正實(shí)根
∵![]()
∴當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞增,不符合題意.
上單調(diào)遞增,不符合題意.
當(dāng)![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() 時(shí),
時(shí),![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
又∵![]() ,當(dāng)
,當(dāng)![]() →
→![]() 時(shí),
時(shí),![]() →
→![]()
∴![]()
∴![]()
綜上,![]() 的取值范圍是
的取值范圍是![]() .
.
(Ⅱ)![]() .
.
∵![]() 有三個(gè)極值點(diǎn)
有三個(gè)極值點(diǎn)
∴![]() 有三個(gè)零點(diǎn),1為一個(gè)零點(diǎn),其他兩個(gè)則為
有三個(gè)零點(diǎn),1為一個(gè)零點(diǎn),其他兩個(gè)則為![]() 的零點(diǎn),由(Ⅰ)知
的零點(diǎn),由(Ⅰ)知![]() .
.
∵![]()
∴![]() 的兩個(gè)零點(diǎn)即為
的兩個(gè)零點(diǎn)即為![]() 的最小和最大極值點(diǎn)
的最小和最大極值點(diǎn)![]() ,
,![]() ,即
,即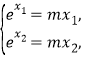 .
.
∴![]()
令![]() ,由題知
,由題知![]() .
.
∴![]() ,
,![]() ,
,![]()
∴![]()
令![]() ,
,![]() ,則
,則![]() ,令
,令![]() ,則
,則![]() .
.
∴![]() 在
在![]() 上單調(diào)遞增
上單調(diào)遞增
∴![]()
∴![]() 在
在![]() 上單調(diào)遞減
上單調(diào)遞減
∴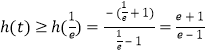
故![]() 的最小值為
的最小值為![]() .
.


 學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案
學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案 Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司為了適應(yīng)市場(chǎng)需求對(duì)產(chǎn)品結(jié)構(gòu)做了重大調(diào)整,調(diào)整后初期利潤增長迅速,之后增長越來越慢,若要建立恰當(dāng)?shù)暮瘮?shù)模型來反映該公司調(diào)整后利潤![]() 與時(shí)間
與時(shí)間![]() 的關(guān)系,可選用
的關(guān)系,可選用
A.一次函數(shù)B.二次函數(shù)
C.指數(shù)型函數(shù)D.對(duì)數(shù)型函數(shù)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在吸煙與患肺病是否相關(guān)的判斷中,有下面的說法:
(1)從獨(dú)立性分析可知在犯錯(cuò)誤的概率不超過0.05的前提下,認(rèn)為吸煙與患肺病有關(guān)系時(shí),是指有![]() 的可能性使得推斷錯(cuò)誤.
的可能性使得推斷錯(cuò)誤.
(2)從獨(dú)立性分析可知在犯錯(cuò)誤的概率不超過0.01的前提下,認(rèn)為吸煙與患肺病有關(guān)系時(shí),若某人吸煙,則他有![]() 的可能患有肺病;
的可能患有肺病;
(3)若![]() ,則在犯錯(cuò)誤的概率不超過0.01的前提下,認(rèn)為吸煙與患肺病有關(guān)系,那么在100個(gè)吸煙的人中必有99人患有肺病;
,則在犯錯(cuò)誤的概率不超過0.01的前提下,認(rèn)為吸煙與患肺病有關(guān)系,那么在100個(gè)吸煙的人中必有99人患有肺病;
其中說法正確的是________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其導(dǎo)函數(shù)為
,其導(dǎo)函數(shù)為![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() ,關(guān)于
,關(guān)于![]() 的不等式
的不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于函數(shù)![]() ,如果存在實(shí)數(shù)
,如果存在實(shí)數(shù)![]() 使得
使得![]() ,那么稱
,那么稱![]() 為
為![]() 的生成函數(shù).
的生成函數(shù).
(1)函數(shù)![]() ,是否為
,是否為![]() 的生成函數(shù)?說明理由;
的生成函數(shù)?說明理由;
(2)設(shè)![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時(shí)生成函數(shù)
時(shí)生成函數(shù)![]() ,求
,求![]() 的對(duì)稱中心(不必證明);
的對(duì)稱中心(不必證明);
(3)設(shè)![]() ,
,![]() ,取
,取![]() ,
,![]() ,生成函數(shù)
,生成函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 的最小值是5,求實(shí)數(shù)
的最小值是5,求實(shí)數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=-2sin2x+sin 2x+1,給出下列四個(gè)命題:
①在區(qū)間![]() 上是減函數(shù);
上是減函數(shù);
②直線![]() 是函數(shù)圖象的一條對(duì)稱軸;
是函數(shù)圖象的一條對(duì)稱軸;
③函數(shù)f(x)的圖象可由函數(shù)![]() 的圖象向左平移
的圖象向左平移![]() 而得到;
而得到;
④若![]() ,則f(x)的值域是
,則f(x)的值域是![]() .
.
其中正確命題序號(hào)是________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=![]() x2-aln x(a∈R).
x2-aln x(a∈R).
(1)若f(x)在x=2處取得極值,求a的值;
(2)求f(x)的單調(diào)區(qū)間;
(3)求證:當(dāng)x>1時(shí), ![]() x2+ln x<
x2+ln x<![]() x3.
x3.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)集![]() 具有性質(zhì)
具有性質(zhì)![]() ;對(duì)任意的
;對(duì)任意的![]() 、
、![]() ,
,![]() ,與
,與![]() 兩數(shù)中至少有一個(gè)屬于
兩數(shù)中至少有一個(gè)屬于![]() .
.
(1)分別判斷數(shù)集![]() 與
與![]() 是否具有性質(zhì)
是否具有性質(zhì)![]() ,并說明理由;
,并說明理由;
(2)證明:![]() ,且
,且![]() ;
;
(3)當(dāng)![]() 時(shí),若
時(shí),若![]() ,求集合
,求集合![]() .
.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com