
【題目】已知定義在![]() 上的函數
上的函數![]() 滿足:對任意
滿足:對任意![]() 都有
都有![]() .
.
(1)求證:函數![]() 是奇函數;
是奇函數;
(2)如果當![]() 時,有
時,有![]() ,試判斷
,試判斷![]() 在
在![]() 上的單調性,并用定義證明你的判斷;
上的單調性,并用定義證明你的判斷;
(3)在(2)的條件下,若![]() 對滿足不等式
對滿足不等式![]() 的任意
的任意![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見解析(2)函數![]() 在
在![]() 上為增函數,證明見解析(3)
上為增函數,證明見解析(3)![]()
【解析】
(1)先分析定義域是否關于原點對稱,再賦值求![]() ,令
,令![]() 即可求證(2)先判斷
即可求證(2)先判斷![]() 在
在![]() 上為增函數,再根據定義證明在
上為增函數,再根據定義證明在![]() 上是奇函數,根據奇函數性質知
上是奇函數,根據奇函數性質知![]() 在
在![]() 上為增函數(3)根據(2)可得不等式
上為增函數(3)根據(2)可得不等式![]() 的解,
的解,![]() 在此范圍恒成立,分離參數即可求解.
在此范圍恒成立,分離參數即可求解.
(1)函數![]() 的定義域
的定義域![]() 關于原點對稱,令
關于原點對稱,令![]() ,可得
,可得![]() ,
,
所以![]() ,令
,令![]() ,則
,則![]() ,即
,即![]() ,所以函數為奇函數.
,所以函數為奇函數.
(2)函數![]() 在
在![]() 上為增函數.
上為增函數.
證明如下:
設![]() 且
且![]() ,則
,則![]()
![]() ,
,
因為![]() 時,有
時,有![]() ,
,
所以![]() ,
,
故![]()
即![]() ,
,
所以函數![]() 在
在![]() 上是增函數,
上是增函數,
根據奇函數的性質知函數![]() 在
在![]() 上是增函數,
上是增函數,
故![]() 在
在![]() 上為增函數.
上為增函數.
(3)因為![]() ,
,
所以![]() ,
,
因為![]() 在
在![]() 上為增函數,
上為增函數,
所以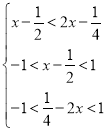 ,解得
,解得![]() .
.
即當![]() 時,
時,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上恒成立,
上恒成立,
而![]() ,
,
所以只需![]() ,
,
故![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知邊長為 ![]() 的菱形ABCD中,∠BAD=60°,沿對角線BD折成二面角A﹣BD﹣C為120°的四面體ABCD,則四面體的外接球的表面積為( )
的菱形ABCD中,∠BAD=60°,沿對角線BD折成二面角A﹣BD﹣C為120°的四面體ABCD,則四面體的外接球的表面積為( )
A.25π
B.26π
C.27π
D.28π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產的某批產品的銷售量![]() 萬件(生產量與銷售量相等)與促銷費用
萬件(生產量與銷售量相等)與促銷費用![]() 萬元滿足
萬元滿足![]() (其中
(其中![]() ,
,![]() 為正常數).已知生產該批產品還需投入成本
為正常數).已知生產該批產品還需投入成本![]() 萬元(不含促銷費用),產品的銷售價格定為
萬元(不含促銷費用),產品的銷售價格定為![]() 元/件
元/件
(1)將該產品的利潤![]() 萬元表示為促銷費用
萬元表示為促銷費用![]() 萬元的函數;(注:利潤=銷售收入-促銷費-投入成本)
萬元的函數;(注:利潤=銷售收入-促銷費-投入成本)
(2)當促銷費用投入多少萬元時,該公司的利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)已知函數f(x)=![]()
(1)判斷函數在區間[1,+∞)上的單調性,并用定義證明你的結論.
(2)求該函數在區間[1,4]上的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax﹣lnx,a∈R.
(1)求函數f(x)的單調區間;
(2)當x∈(0,e]時,求g(x)=e2x﹣lnx的最小值;
(3)當x∈(0,e]時,證明:e2x﹣lnx﹣ ![]() >
> ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查某地區老人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
性別 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估計該地區老年人中,需要志愿者提供幫助的老年人的比例;
(2)請根據上面的數據分析該地區的老年人需要志愿者提供幫助與性別有關嗎
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,g(x)= ![]() (其中a∈R)
(其中a∈R)
(1)求函數f(x)的極值;
(2)設函數h(x)=f′(x)+g(x)﹣1,試確定h(x)的單調區間及最值;
(3)求證:對于任意的正整數n,均有 ![]() >
> ![]() 成立.(注:e為自然對數的底數)
成立.(注:e為自然對數的底數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com