
 ,其中{an}、{bn}分別為等差數列和等比數列,O為坐標原點,若P1是線段AB的中點.
,其中{an}、{bn}分別為等差數列和等比數列,O為坐標原點,若P1是線段AB的中點.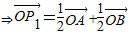 ,
,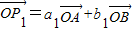 ,且
,且 不共線,由平面向量基本定理,能求出a1,b1的值.
不共線,由平面向量基本定理,能求出a1,b1的值.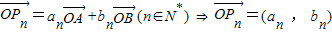 ,設{an}的公差為d,{bn}的公比為q,則由于P1,P2,P3,…,Pn,…互不相同,所以d=0,q=1不會同時成立;若d=0,則
,設{an}的公差為d,{bn}的公比為q,則由于P1,P2,P3,…,Pn,…互不相同,所以d=0,q=1不會同時成立;若d=0,則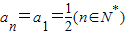 ,所以P1,P2,P3,…,Pn,…都在直線
,所以P1,P2,P3,…,Pn,…都在直線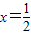 上.由此能求出當d≠0且q≠1時,P1,P2,P3,…,Pn,…不共線.
上.由此能求出當d≠0且q≠1時,P1,P2,P3,…,Pn,…不共線. 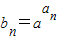
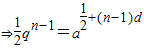 .令n=1,則
.令n=1,則 ,于是,
,于是,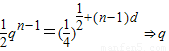 有唯一解
有唯一解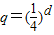 .由此能夠得到當對于給定的{an},都能找到唯一的一個{bn},使得P1,P2,P3,…,Pn,…,都在指數函數
.由此能夠得到當對于給定的{an},都能找到唯一的一個{bn},使得P1,P2,P3,…,Pn,…,都在指數函數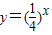 的圖象上.
的圖象上.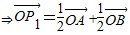 …(1分)
…(1分)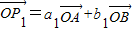 ,且
,且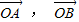 不共線,
不共線,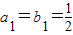 …(3分)
…(3分)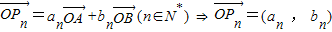
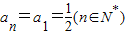 ,⇒P1,P2,P3,…,Pn,…都在直線
,⇒P1,P2,P3,…,Pn,…都在直線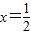 上; …(5分)
上; …(5分)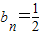 為常數列,⇒P1,P2,P3,…,Pn,…都在直線
為常數列,⇒P1,P2,P3,…,Pn,…都在直線 上; …(6分)
上; …(6分)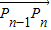 =(an-an-1,bn-bn-1)與
=(an-an-1,bn-bn-1)與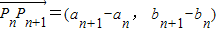 共線(n>1,n∈N*)?(an-an-1)(bn+1-bn)-(an+1-an)(bn-bn-1)=0?d(bn+1-bn)-d(bn-bn-1)=0?(bn+1-bn)=(bn-bn-1)?q=1與q≠1矛盾,
共線(n>1,n∈N*)?(an-an-1)(bn+1-bn)-(an+1-an)(bn-bn-1)=0?d(bn+1-bn)-d(bn-bn-1)=0?(bn+1-bn)=(bn-bn-1)?q=1與q≠1矛盾,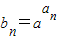
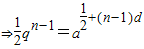 (10分)
(10分)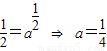 ,…(11分)
,…(11分)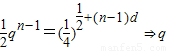 有唯一解
有唯一解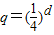 ,…(13分)
,…(13分)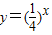 的圖象上.…(14分)
的圖象上.…(14分)

 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:高中數學 來源: 題型:
 如圖,已知點A(-1,0)與點B(1,0),C是圓x2+y2=1上的動點,連接BC并延長至D,使得|CD|=|BC|,求AC與OD的交點P的軌跡方程.
如圖,已知點A(-1,0)與點B(1,0),C是圓x2+y2=1上的動點,連接BC并延長至D,使得|CD|=|BC|,求AC與OD的交點P的軌跡方程.查看答案和解析>>
科目:高中數學 來源: 題型:
| OPn |
| OA |
| OB |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com