
(2006
江西,21)如圖所示,橢圓 (a>b>0)的右焦點為F(c,0),過點F的一動直線m繞點F轉動,并且交橢圓于A、B兩點,P為線段AB的中點.
(a>b>0)的右焦點為F(c,0),過點F的一動直線m繞點F轉動,并且交橢圓于A、B兩點,P為線段AB的中點.
(1)
求點P的軌跡H的方程;(2)
若在Q的方程中,令 ,
, .確定θ的值,使原點距橢圓Q的右準線l最遠.此時,設l與x軸交點為D,當直線m繞點F轉動到什么位置時,△ABD的面積最大?
.確定θ的值,使原點距橢圓Q的右準線l最遠.此時,設l與x軸交點為D,當直線m繞點F轉動到什么位置時,△ABD的面積最大?

|
解析: (1)設橢圓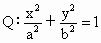 上的點 上的點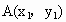 、 、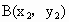 ,又設P點坐標為P(x,y), ,又設P點坐標為P(x,y),
則 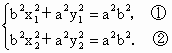
(i) 當AB不垂直x軸時,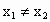 , ,
由①-②得
∴ 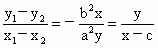 , ,
∴ 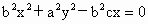 (*) (*)
(ii) 當AB垂直于x軸時,點P即為點F,滿足方程(*),故所求點 P的軌跡H的方程為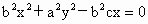 . .
(2) 因為橢圓Q右準線l方程是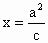 ,原點距橢圓Q的右準線l的距離為 ,原點距橢圓Q的右準線l的距離為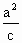 ,由于 ,由于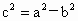 , ,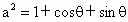 , ,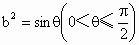 . .
則 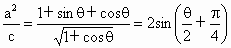 . .
當  時,上式達到最大值,所以當 時,上式達到最大值,所以當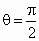 時,原點距橢圓Q的右準線l最遠.此時 時,原點距橢圓Q的右準線l最遠.此時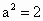 , ,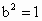 ,c=1,D(2,0),|DF|=1. ,c=1,D(2,0),|DF|=1.
設橢圓 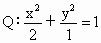 上的點 上的點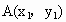 、 、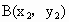 , ,
△ ABD面積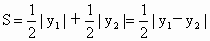 . .
設直線 m的方程為x=ky+1,代入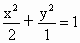 中, 中,
得 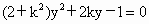 . .
由韋達定理得 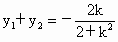 , ,
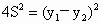 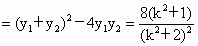 , ,
令 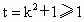 ,得 ,得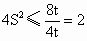 ,當t=1,即k=0時取等號. ,當t=1,即k=0時取等號.
因此,當直線 m繞點F轉動到垂直x軸位置時,三角形ABD的面積最大. |


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com