
【題目】2018年9月16日下午5時左右,今年第22號臺風“山竹”在廣東江門川島鎮附近正面登陸,給當地人民造成了巨大的財產損失,某記者調查了當地某小區的100戶居民由于臺風造成的經濟損失,將收集的數據分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五組,并作出如下頻率分布直方圖.
五組,并作出如下頻率分布直方圖.
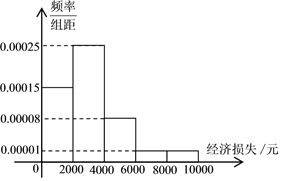
(Ⅰ)根據頻率分布直方圖估計該小區居民由于臺風造成的經濟損失的眾數和平均值.
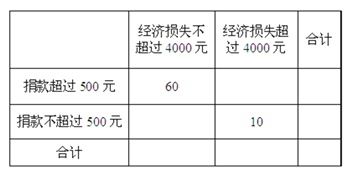
(Ⅱ)“一方有難,八方支援”,臺風后居委會號召小區居民為臺風重災區捐款,![]() 記者調查的100戶居民捐款情況如下表格,在表格空白處填寫正確數字,并說明是否有99%以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4000元有關?
記者調查的100戶居民捐款情況如下表格,在表格空白處填寫正確數字,并說明是否有99%以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4000元有關?
(Ⅲ)將上述調查所得到的頻率視為概率,現在從該地區大量受災居民中,采用隨機抽樣方法每次抽取1戶居民,抽取3次,記被抽取的3戶居民中自身經濟損失超過![]() 元的人數為
元的人數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列及期望
的分布列及期望![]() .
.
參考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
【答案】(Ⅰ)眾數為3000,平均值為2920(Ⅱ)沒有把握(Ⅲ)詳見解析
【解析】
(Ⅰ)最高矩形中點橫坐標就是眾數,每個矩形的中點橫坐標與該矩形的縱坐標、組距相乘后求和可得平均值;(Ⅱ)根據直方圖得到列聯表,利用公式求得![]() ,與鄰界值比較,即可得到結論;(Ⅲ)
,與鄰界值比較,即可得到結論;(Ⅲ)![]() 的取值可能有
的取值可能有![]() ,根據獨立重復試驗概率公式求出各隨機變量對應的概率,從而可得分布列,利用二項分布的期望公式可得結果.
,根據獨立重復試驗概率公式求出各隨機變量對應的概率,從而可得分布列,利用二項分布的期望公式可得結果.
(Ⅰ)根據頻率分布直方圖知該小區居民由于臺風造成的經濟損失的眾數=3000(元);
平均值=![]() (元)
(元)
(Ⅱ)由頻率分布直方圖可知,在抽取的100人中,經濟損失不超過![]() 元的有
元的有![]() 人,經濟損失超過
人,經濟損失超過![]() 元的有100-80=20人,
元的有100-80=20人,
則表格數據如下
經濟損失不 超過4000元 | 經濟損失超 過4000元 | 合計 | |
捐款超過500元 | 60 | 10 | 70 |
捐款不超過500元 | 20 | 10 | 30 |
合計 | 80 | 20 | 100 |
![]() .
.
由于![]() ,
,![]()
所以沒有99%以上的把握認為捐款數額是否多于或少于500元和自身經濟損失是否到4000元有關.
(Ⅲ)由頻率分布直方圖可知抽到自身經濟損失超過![]() 元居民的頻率為
元居民的頻率為![]() ,將頻率視為概率. 由題意知
,將頻率視為概率. 由題意知![]() 的取值可能有
的取值可能有![]() ,
,
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的分布列
的分布列
![]()


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
【題目】已知![]() 和
和![]() 是橢圓
是橢圓![]() 的兩個焦點,且點
的兩個焦點,且點![]() 在橢圓C上.
在橢圓C上.
(1)求橢圓C的方程;
(2)直線![]() (m>0)與橢圓C有且僅有一個公共點,且與x軸和y軸分別交于點M,N,當△OMN面積取最小值時,求此時直線
(m>0)與橢圓C有且僅有一個公共點,且與x軸和y軸分別交于點M,N,當△OMN面積取最小值時,求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
某初級中學共有學生2000名,各年級男、女生人數如下表:
初一年級 | 初二年級 | 初三年級 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校學生中隨機抽取1名,抽到初二年級女生的概率是0.19.
求x的值;
現用分層抽樣的方法在全校抽取48名學生,問應在初三年級抽取多少名?
已知y![]() 245,z
245,z![]() 245,求初三年級中女生比男生多的概率.
245,求初三年級中女生比男生多的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要測量底部不能到達的電視塔AB的高度,在C點測得塔頂A的仰角是45°,在D點測得塔頂A的仰角是30°,并測得水平面上的∠BCD=120°,CD="40" m,則電視塔的高度為多少?
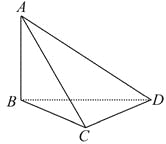
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知實數![]() ,定義域為
,定義域為![]() 的函數
的函數![]() 是偶函數,其中
是偶函數,其中![]() 為自然對數的底數.
為自然對數的底數.
(Ⅰ)求實數![]() 值;
值;
(Ⅱ)判斷該函數![]() 在
在![]() 上的單調性并用定義證明;
上的單調性并用定義證明;
(Ⅲ)是否存在實數![]() ,使得對任意的
,使得對任意的![]() ,不等式
,不等式![]() 恒成立.若存在,求出實數
恒成立.若存在,求出實數![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() ,其右焦點為
,其右焦點為![]() .點
.點![]() 是橢圓
是橢圓![]() 上異于長軸端點的任意一點,連接
上異于長軸端點的任意一點,連接![]() 并延長交橢圓
并延長交橢圓![]() 于點
于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且直線
為坐標原點,且直線![]() 與右準線
與右準線![]() 交于點
交于點![]() .
.
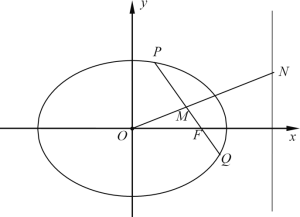
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,
, ![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 與
與![]() 的交點的軌跡
的交點的軌跡![]() 的方程;
的方程;
(2)若曲線![]() 上存在4個點到直線
上存在4個點到直線![]() 的距離相等,求實數
的距離相等,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com