
如圖,在底面為平行四邊形的四棱柱 中,
中,
 底面
底面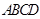 ,
, ,
, ,
, .
.
(1)求證:平面 平面
平面 ;
;
(2)若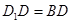 ,求四棱錐
,求四棱錐 的體積.
的體積.
(1)詳見解析;(2)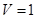 .
.
解析試題分析:(1)由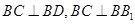 得:
得: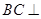 平面
平面 ,進而證得面面垂直;(2)法1:做出底面的垂線,證明線面垂直,再利用體積公式;法2:分割法轉化成兩個三棱錐的體積之和,再利用轉換頂點的求三棱錐的體積,再相加求四棱錐的體積(省去找底面的垂線)
,進而證得面面垂直;(2)法1:做出底面的垂線,證明線面垂直,再利用體積公式;法2:分割法轉化成兩個三棱錐的體積之和,再利用轉換頂點的求三棱錐的體積,再相加求四棱錐的體積(省去找底面的垂線)
試題解析:(1)證明: 在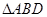 中,由余弦定理得:
中,由余弦定理得: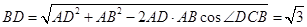 ,
,
所以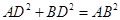 ,所以
,所以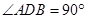 ,即
,即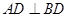 , 3分
, 3分
又四邊形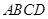 為平行四邊形,所以
為平行四邊形,所以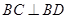 ,
,
又
 底面
底面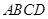 ,
,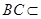 底面
底面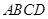 ,所以
,所以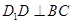 , 4分
, 4分
又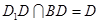 ,所以
,所以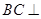 平面
平面 , 5分
, 5分
又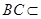 平面
平面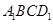 ,所以平面
,所以平面 平面
平面 . 6分
. 6分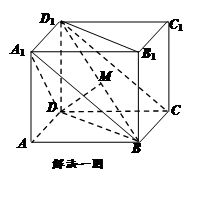
(2)法一:連結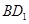 ,∵
,∵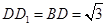 ,∴
,∴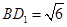
∵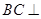 平面
平面 ,所以
,所以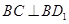 , 8分
, 8分
所以四邊形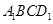 的面積
的面積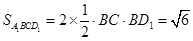 , 10分
, 10分
取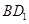 的中點
的中點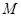 ,連結
,連結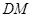 ,則
,則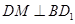 ,且
,且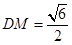 ,
,
又平面 平面
平面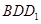 ,平面
,平面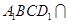 平面
平面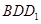
 ,
,
所以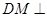 平面
平面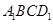 , 13分
, 13分
所以四棱錐 的體積:
的體積: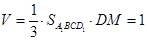 . 14分
. 14分
法二: 四棱錐 的體積
的體積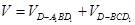 , 8分
, 8分
而三棱錐 與三棱錐
與三棱錐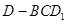 底面積和高均相等, 10分
底面積和高均相等, 10分
所以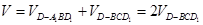
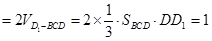 . 14分
. 14分
考點:1.面面垂直;2.線面垂直;3等體積法求錐體的體積


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
如圖,在六面體ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1. (1)求證:BF∥平面ACGD; (2)求二面角DCGF的余弦值.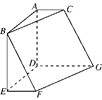
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知多面體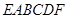 的底面
的底面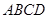 是邊長為
是邊長為 的正方形,
的正方形,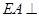 底面
底面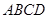 ,
,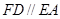 ,且
,且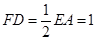 .
.
(Ⅰ)求多面體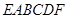 的體積;
的體積;
(Ⅱ)求直線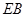 與平面
與平面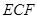 所成角的正弦值;
所成角的正弦值;
(Ⅲ)記線段BC的中點為K,在平面ABCD內過點K作一條直線與平面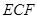 平行,要求保留作圖痕跡,但不要求證明.
平行,要求保留作圖痕跡,但不要求證明.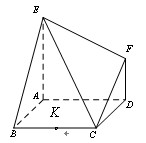
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在各棱長均為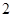 的三棱柱
的三棱柱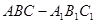 中,側面
中,側面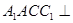 底面
底面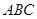 ,
,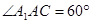 .
.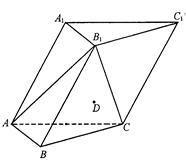
(1)求側棱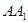 與平面
與平面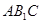 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)已知點 滿足
滿足 ,在直線
,在直線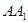 上是否存在點
上是否存在點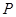 ,使
,使 ?若存在,請確定點
?若存在,請確定點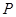 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com