
已知函數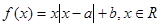 .
.
(1)當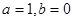 時,判斷
時,判斷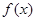 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(2)當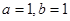 時,若
時,若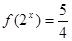 ,求
,求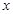 的值;
的值;
(3)若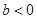 ,且對任何
,且對任何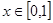 不等式
不等式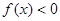 恒成立,求實數
恒成立,求實數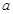 的取值范圍.
的取值范圍.
(1)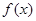 既不是奇函數,也不是偶函數;(2)所以
既不是奇函數,也不是偶函數;(2)所以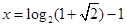 或
或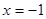 ;(3)當
;(3)當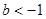 時,
時,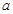 的取值范圍是
的取值范圍是 ,當
,當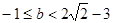 時,
時,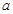 的取值范圍是
的取值范圍是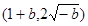 ;當
;當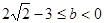 時,
時,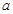 的取值范圍是
的取值范圍是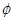 .
.
【解析】
試題分析:(1)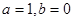 時,
時,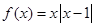 為確定的函數,要證明它具有奇偶性,必須按照定義證明,若要說明它沒有奇偶性,可舉一特例,說明某一對值
為確定的函數,要證明它具有奇偶性,必須按照定義證明,若要說明它沒有奇偶性,可舉一特例,說明某一對值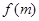 與
與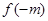 不相等(不是偶函數)也不相反(不是奇函數).(2)當
不相等(不是偶函數)也不相反(不是奇函數).(2)當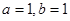 時,
時,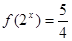 為
為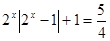 ,這是含有絕對值符號的方程,要解這個方程一般是分類討論絕對值符號里的式子
,這是含有絕對值符號的方程,要解這個方程一般是分類討論絕對值符號里的式子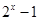 的正負,以根據絕對值定義去掉絕對值符號,變成通常的方程來解.(3)不等式
的正負,以根據絕對值定義去掉絕對值符號,變成通常的方程來解.(3)不等式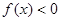 恒成立時要求參數
恒成立時要求參數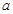 的取值范圍,一般要把問題進行轉化,例如分離參數法,或者轉化為函數的最值問題.
的取值范圍,一般要把問題進行轉化,例如分離參數法,或者轉化為函數的最值問題.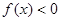 即為
即為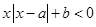 ,可以先把絕對值式子
,可以先把絕對值式子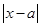 解出來,這時注意首先把
解出來,這時注意首先把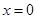 分出來,然后討論
分出來,然后討論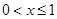 時,不等式化為
時,不等式化為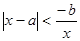 ,于是有
,于是有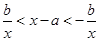 ,即
,即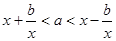 ,這個不等式恒成立,說明
,這個不等式恒成立,說明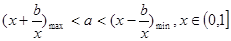 ,這時我們的問題就轉化為求函數
,這時我們的問題就轉化為求函數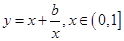 的最大值,求函數
的最大值,求函數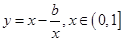 的最小值.
的最小值.
試題解析:(1)當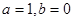 時,
時,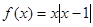 既不是奇函數也不是偶函數(2分)
既不是奇函數也不是偶函數(2分)
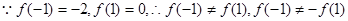
所以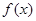 既不是奇函數,也不是偶函數 (4分)
既不是奇函數,也不是偶函數 (4分)
(2)當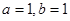 時,
時,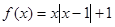 ,
,
由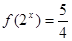 得
得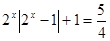 (1分)
(1分)
即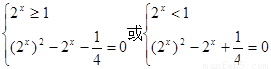 (3分)
(3分)
解得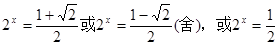 (5分)
(5分)
所以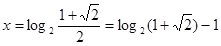 或
或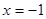 (6分)
(6分)
(3)當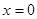 時,
時,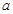 取任意實數,不等式
取任意實數,不等式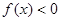 恒成立,
恒成立,
故只需考慮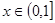 ,此時原不等式變為
,此時原不等式變為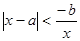 (1分)
(1分)
即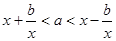
故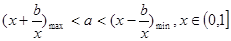
又函數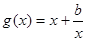 在
在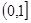 上單調遞增,所以
上單調遞增,所以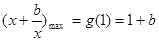 ;(2分)
;(2分)
對于函數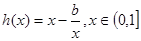
①當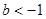 時,在
時,在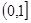 上
上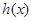 單調遞減,
單調遞減,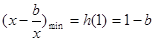 ,又
,又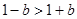 ,
,
所以,此時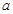 的取值范圍是
的取值范圍是 (3分)
(3分)
②當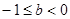 ,在
,在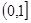 上,
上,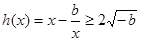 ,
,
當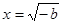 時,
時,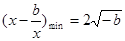 ,此時要使
,此時要使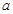 存在,
存在,
必須有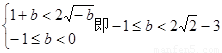 ,此時
,此時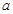 的取值范圍是
的取值范圍是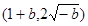 (4分)
(4分)
綜上,當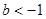 時,
時,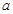 的取值范圍是
的取值范圍是
當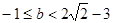 時,
時,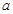 的取值范圍是
的取值范圍是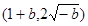 ;
;
當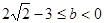 時,
時,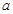 的取值范圍是
的取值范圍是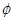 (6分)
(6分)
考點:(1)函數的奇偶性;(2)含絕對值的方程;(2)含參數的不等式恒成立問題.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源:2013-2014學年廣東省深圳市寶安區高三上學期調研考試文科數學試卷(解析版) 題型:解答題
已知函數 ,
,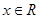 .
.
(1)當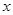 為何值時,
為何值時,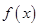 取得最大值,并求出其最大值;
取得最大值,并求出其最大值;
(2)若 ,
,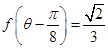 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建省高三5月高考三輪模擬文科數學試卷(解析版) 題型:解答題
已知函數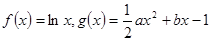 ,
,
(1)當 且
且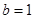 時,證明:對
時,證明:對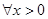 ,
,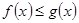 ;
;
(2)若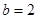 ,且
,且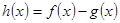 存在單調遞減區間,求
存在單調遞減區間,求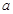 的取值范圍;
的取值范圍;
(3)數列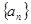 ,若存在常數
,若存在常數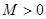 ,
,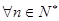 ,都有
,都有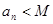 ,則稱數列
,則稱數列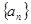 有上界。已知
有上界。已知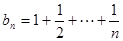 ,試判斷數列
,試判斷數列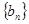 是否有上界.
是否有上界.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三第三次模擬考試理科數學試卷(解析版) 題型:解答題
已知函數 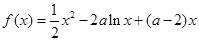 ,
,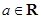 .
.
(1)當 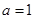 時,求函數
時,求函數 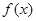 的最小值;
的最小值;
(2)當 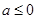 時,討論函數
時,討論函數 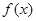 的單調性;
的單調性;
(3)是否存在實數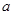 ,對任意的
,對任意的
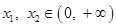 ,且
,且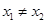 ,有
,有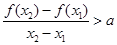 ,恒成立,若存在求出
,恒成立,若存在求出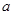 的取值范圍,若不存在,說明理由。
的取值范圍,若不存在,說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com