
已知定義在R上的二次函數R(x)=ax2+bx+c滿足2 R(﹣x)﹣2 R(x)=0,且R(x)的最小值為0,函數h(x)=lnx,又函數f(x)=h(x)﹣R(x).
(I)求f(x)的單調區間;
(II)當a≤ 時,若x0∈[1,3],求f(x0)的最小值;
時,若x0∈[1,3],求f(x0)的最小值;
(III)若二次函數R(x)圖象過(4,2)點,對于給定的函數f(x)圖象上的點A(x1,y1),當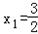 時,探求函數f(x)圖象上是否存在點B(x2,y2)(x2>2),使A、B連線平行于x軸,并說明理由.(參考數據:e=2.71828…)
時,探求函數f(x)圖象上是否存在點B(x2,y2)(x2>2),使A、B連線平行于x軸,并說明理由.(參考數據:e=2.71828…)
解:(I)∵定義在R上的二次函數R(x)=ax2+bx+c滿足2 R(﹣x)﹣2 R(x)=0,
∴2 R(﹣x)﹣2 R(x)=0,
∴2 R(﹣x)=2R(x),即R(﹣x)=R(x),
∵R(x)=ax2+bx+c,
∴b=0,
∴R(x)=ax2+c.
∵R(x)=ax2+c的最小值為0,
∴a>0,c=0,故R(x)=ax2,
∵R(x)=ax2,h(x)=lnx,f(x)=h(x)﹣R(x),
∴f(x)=lnx﹣ax2,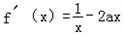 ,
,
令f'(x)=0,解得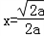 .
.
當x變化時,f'(x),f(x)的變化情況如下表:
f(x)的單調遞減區間是(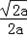 ,+∞).
,+∞).
(II)∵當0<a≤ 時,
時,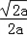 ≥1,
≥1,
∴x0∈[1,3]時,f(x0)的最小值為f(1)與f(3)中的較小者.
又f(1)=﹣a,f(3)=1n3﹣9a,f(1)﹣f(3)=﹣a﹣(ln3﹣9a)=8a﹣1n3.
∴當0<a≤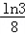 時,f(1)≤f(3),f(x0)的最小值﹣a;
時,f(1)≤f(3),f(x0)的最小值﹣a;
當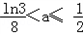 時,f(1)>f(3),f(x0)的最小值ln3﹣9a.
時,f(1)>f(3),f(x0)的最小值ln3﹣9a.
(III)證明:若二次函數R(x)=ax2圖象過(4,2)點,則 ,
,
所以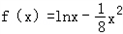 .
.
令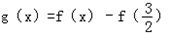 .
.
由(I)知f(x)在(0,2)內單調遞增,
故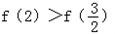 ,即g(2)>0.
,即g(2)>0.
取 ,則
,則 .
.
所以存在 ,使g(x2)=0,
,使g(x2)=0,
故存在x2∈(2,+∞),使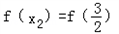 .
.
所以函數f(x)圖象上存在點B(x2,y2)(x2>2),使A、B連線平行于x軸.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | e |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高三第二次質檢理科數學復習卷(二) 題型:解答題
.已知定義在R上的二次函數 滿足
滿足 ,且
,且 的最小值
的最小值
為0,函數 ,又函數
,又函數 。
。
(I)求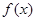 的單調區間; (II)當
的單調區間; (II)當 ≤
≤ 時,若
時,若 ,求
,求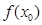 的最小值;
的最小值;
(III)若二次函數 圖象過(4,2)點,對于給定的函數
圖象過(4,2)點,對于給定的函數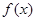 圖象上的點A(
圖象上的點A( ),
),
當 時,探求函數
時,探求函數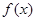 圖象上是否存在點
圖象上是否存在點 (
( )(
)( ),使
),使 、
、 連線平行于
連線平行于 軸,并說明理由。(參考數據:e=2.71828…)
軸,并說明理由。(參考數據:e=2.71828…)
查看答案和解析>>
科目:高中數學 來源:2012屆山東省日照市高三上學期測評理科數學試卷 題型:解答題
已知定義在R上的二次函數 滿足
滿足 ,且
,且 的最小值為0,函數
的最小值為0,函數 ,又函數
,又函數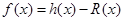 。
。
(I)求 的單調區間;
的單調區間;
(II)當 ≤
≤ 時,若
時,若 ,求
,求 的最小值;
的最小值;
(III)若二次函數 圖象過(4,2)點,對于給定的函數
圖象過(4,2)點,對于給定的函數 圖象上的點A(
圖象上的點A( ),當
),當 時,探求函數
時,探求函數 圖象上是否存在點B(
圖象上是否存在點B( )(
)( ),使A、B連線平行于x軸,并說明理由。
),使A、B連線平行于x軸,并說明理由。
(參考數據:e=2.71828…)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com