，∠BAE=∠BCD=∠CDE=120°.?
(1)求異面直線CD與SB所成的角(用反三角函數(shù)值表示)；?
(2)證明BC⊥平面SAB；?
(3)用反三角函數(shù)值表示二面角B-SC-D的大小.(本小問不必寫出解答過程)
(1)解析：連結(jié)BE，延長BC、ED交于點F，則∠DCF=∠CDF=60°，∴△CDF為正三角形.∴CF=DF.
又BC=DE，∴BF=EF.?
因此，△BFE為正三角形.?
∴∠FBE=∠FCD=60°.?
∴BE∥CD.?
所以∠SBE(或其補角)就是異面直線CD與SB所成的角.?
∵SA⊥底面ABCDE，SA=AB=AE=2，∴SB=2
.?
同理SE=2.?
又∠BAE=120°，所以BE=2
.?
從而cos∠SBE=
,?
∴∠SBE=arccos
.?
所以異面直線CD與SB所成的角是arccos
.?
(2)證明：由題意，△ABE為等腰三角形，∠BAE=120°,?
∴∠ABE=30°.?
又∠FBE=60°，?
∴∠ABC=90°.?
∴BC⊥BA.?
∵SA⊥底面ABCDE，BC
底面ABCDE ，∴SA⊥BC.?
又SA∩BA=A,∴BC⊥平面SAB.?
(3)解析：二面角BSCD的大小為π-arccos
.
科目：高中數(shù)學(xué) 來源： 題型：
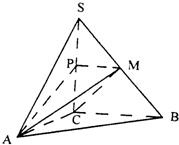如圖，在三棱錐S-ABC中，SC⊥平面ABC，點P、M分別是SC和SB的中點，設(shè)PM=AC=1，∠ACB=90°，直線AM與直線SC所成的角為60°．查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
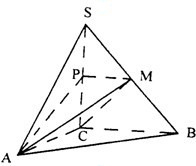如圖，在三棱錐S-ABC中，SC⊥平面ABC，點P、M分別是SC和SB的中點，設(shè)PM=AC=1，∠ACB=90°，直線AM與直線SC所成的角為60°．查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
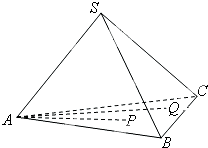如圖，在三棱錐S-ABC中，設(shè)P、Q為底面△ABC內(nèi)的兩點，且| AP |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
| AQ |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
| 4 |
| 5 |
| 4 |
| 5 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
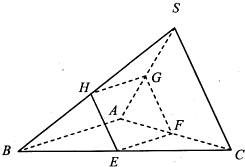（2012•江蘇二模）如圖，在三棱錐S-ABC，平面EFGHBC，CA，AS，SB交與點E，F(xiàn)，G，H，且SA⊥平面EFGH，SA⊥AB，EF⊥FG．查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
（2013•杭州模擬）如圖，在三棱錐S-ABC中，SA=SC=AB=BC，則直線SB與AC所成角的大小是（ ）