
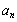 }滿足
}滿足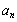 =2
=2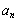 +2n-1(n≥2),且a4=81.
+2n-1(n≥2),且a4=81. (1)求數列的前三項a1,a2,a3.
(2)是否存在一個實數λ,使得數列{![]() }為等差數列?若存在,求出λ的值;若不存在,請說明理由.
}為等差數列?若存在,求出λ的值;若不存在,請說明理由.
(3)求數列{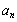 }的前n項和Sn.
}的前n項和Sn.
解:(1)由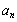 =2
=2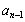 +2n-1(n≥2)
+2n-1(n≥2)![]() a4=
a4=![]() a
a
同理可得a2=13,a1=5. ?
(2)假設存在實數λ符合題意,則![]() -
-![]() 必為與n無關的常數.?
必為與n無關的常數.?
∵![]() -
-![]() =
=![]() =
=![]() =1-
=1-![]() ,要使
,要使![]() -
-![]() 是與n無關的常數,則
是與n無關的常數,則![]() =0,得λ=-1.?
=0,得λ=-1.?
故存在實數λ=-1,使得數列{![]() }為等差數列. ?
}為等差數列. ?
(3)由(2)知數列{![]() }的公差d=1.?
}的公差d=1.?
∴![]() =
=![]() +(n-1)·1=n+1,得
+(n-1)·1=n+1,得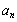 =(n+1)·2n+1.?
=(n+1)·2n+1.?
∵a1=2·21+1,a2=3·22+1,a3=4·23+1,…,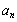 =(n+1)·2n+1,?
=(n+1)·2n+1,?
∴Sn=a1+a2+a3+…+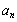 =n+2·2+3·22+4·23+…+(n+1)·2n.?
=n+2·2+3·22+4·23+…+(n+1)·2n.?
記Tn=2·2+3·22+4·23+…+(n+1)·2n,?
有2Tn=2·22+3·23+4·24+…+n·2n+(n+1)·2n+1.?
相減,得Tn=n·2n+1.?
故Sn=n·2n+1+n=n(2n+1+1).


科目:高中數學 來源: 題型:
| 3x-2 |
| 2x-1 |
| 1 |
| 2 |
| 1 |
| 2013 |
| 2 |
| 2013 |
| 3 |
| 2013 |
| 2012 |
| 2013 |
| 2n+1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com