
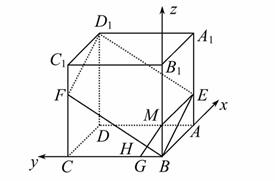
如圖,已知ABCD-A1B1C1D1是棱長為3的正方體,點E在AA1上,點F在CC1上,且AE=FC1=1.

(1)求證:E,B,F,D1四點共面;
(2)若點G在BC上,BG=![]() ,點M在BB1上,GM⊥BF,垂足為H,求證:
,點M在BB1上,GM⊥BF,垂足為H,求證:
EM⊥平面BCC1B1;
(3)用θ表示截面EBFD1和側面BCC1B1所成的銳二面角的大小,求tanθ.
(1)建立如圖所示的空間直角坐標系,
則![]() =(3,0,1),
=(3,0,1),![]() =(0,3,2),
=(0,3,2),![]() =(3,3,3),
=(3,3,3),
所以![]() =
=![]() +
+![]() ,
,
故![]() ,
,![]() ,
,![]() 共面.
共面.
又它們有公共點B,
所以E,B,F,D1四點共面.
(2)設M(0,0,z),則![]() =(0,-
=(0,-![]() ,z),
,z),
而![]() =(0,3,2),
=(0,3,2),
由題設得![]() ·
·![]()
![]() =-
=-![]() ×3+z·2=0,
×3+z·2=0,
得z=1.因為M(0,0,1),E(3,0,1),
有![]() =(3,0,0),
=(3,0,0),
又![]() =(0,0,3),
=(0,0,3),![]() =(0,3,0),
=(0,3,0),
所以![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,
=0,
從而ME⊥BB1,ME⊥BC.
又BB1∩BC=B,
故ME⊥平面BCC1B1.
(3)設向量![]() =(x,y,3)且BP⊥截面EBFD1,
=(x,y,3)且BP⊥截面EBFD1,
于是![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() .
.
而![]() =(3,0,1),
=(3,0,1),![]() =(0,3,2),
=(0,3,2),
得![]() ·
·![]() =3x+3=0,
=3x+3=0,![]() ·
·![]() =3y+6=0,
=3y+6=0,
解得x=-1,y=-2,
所以![]() =(-1,-2,3).
=(-1,-2,3).
又![]() =(3,0,0)且BA⊥平面BCC1B1,
=(3,0,0)且BA⊥平面BCC1B1,
所以![]() 和
和![]() 的夾角等于θ或π-θ(θ為銳角).
的夾角等于θ或π-θ(θ為銳角).
于是cosθ=![]() =
=![]() .
.
故tanθ=![]() .
.


科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•汕頭二模)如圖,已知ABCD-A1B1C1D1是底面邊長為1的正四棱柱,
(2012•汕頭二模)如圖,已知ABCD-A1B1C1D1是底面邊長為1的正四棱柱,查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如圖,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2005•普陀區一模)如圖,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若將圖中已作出的線段的兩個端點分別作為向量的始點和終點所形成的不相等的向量的全體構成集合M,則從集合M中任取兩個向量恰為平行向量的概率是
(2005•普陀區一模)如圖,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若將圖中已作出的線段的兩個端點分別作為向量的始點和終點所形成的不相等的向量的全體構成集合M,則從集合M中任取兩個向量恰為平行向量的概率是| 2 |
| 15 |
| 2 |
| 15 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com