
【題目】若實數x、y、m滿足|x﹣m|<|y﹣m|,則稱x比y接近m.
(1)若2x比1接近3,求x的取值范圍;
(2)已知函數f(x)定義域D=(﹣∞,0)∪(0,1)∪(1,3)∪(3,+∞),對于任意的x∈D,f(x)等于x2﹣2x與x中接近0的那個值,寫出函數f(x)的解析式,若關于x的方程f(x)﹣a=0有兩個不同的實數根,求出a的取值范圍;
(3)已知a,b∈R,m>0且a≠b,求證: ![]() 比
比 ![]() 接近0.
接近0.
【答案】
(1)解:因為2x比1接近3,所以|2x﹣3|<|1﹣3|,
即|2x﹣3|<2,解得 ![]() <x<
<x< ![]() ,
,
所以,x的取值范圍為:( ![]() ,
, ![]() )
)
(2)解:分類討論如下:
①當x2﹣2x比x接近于0時,|x2﹣2x|<|x|,
解得,x∈(1,3),
②當x比x2﹣2x接近于0時,|x2﹣2x|>|x|,
解得,x∈(﹣∞,0)∪(0,1)∪(3,+∞),
所以,f(x)= ![]() ,
,
畫出f(x)的圖象,如下圖,

因為方程f(x)=a有兩個實根,根據函數圖象得,
a∈(﹣1,0)∪(0,1)
(3)解:對兩式 ![]() ,
, ![]() 平方作差得,
平方作差得,
△=( ![]() )2﹣(
)2﹣( ![]() )2
)2
= ![]() =
= ![]() ,
,
因為a,b∈R,m>0且a≠b,所以,△>0恒成立,
所以, ![]() >|
>| ![]() |,
|,
即 ![]() 比
比 ![]() 接近0.
接近0.
【解析】(1)直接根據定義,問題等價為|2x﹣3|<|1﹣3|,解出即可;(2)先求出函數f(x)的解析式并畫出函數圖象,再運用數形結合的方法,求a的取值范圍;(3)直接運用作差法比較兩式的大小.
【考點精析】解答此題的關鍵在于理解絕對值不等式的解法的相關知識,掌握含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規律:關鍵是去掉絕對值的符號.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點.
的中點.

(1)求四棱錐![]() 的體積;
的體積;
(2)求證: ![]() ;
;
(3)判斷線段![]() 上是否存在一點
上是否存在一點![]() (與點
(與點![]() 不重合),使得
不重合),使得![]() 四點共面? (結論不要求證明)
四點共面? (結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sinx,若存在x1 , x2 , …,xn滿足0≤x1<x2<…<xn≤nπ,n∈N+ , 且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…+|f(xm﹣1)﹣f(xm)|=12,(m≥2,m∈N+),當m取最小值時,n的最小值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 的圖像經過點
的圖像經過點![]() ,且滿足
,且滿足![]() ,
,
(1)求![]() 的解析式;
的解析式;
(2)已知![]() ,求函數
,求函數![]() 在
在![]() 的最大值和最小值;
的最大值和最小值;
函數![]() 的圖像上是否存在這樣的點,其橫坐標是正整數,縱坐標是一個完全平方數?如果存在,求出這樣的點的坐標;如果不存在,請說明理由
的圖像上是否存在這樣的點,其橫坐標是正整數,縱坐標是一個完全平方數?如果存在,求出這樣的點的坐標;如果不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)是定義在(0,+∞)上的增函數,且對一切x,y>0,滿足![]() .
.
(1)求f(1)的值;
(2)若f(6)=1,解不等式f(x+3)-f(![]() )<2.
)<2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(ax2-x+1)(a>0,a≠1).
(1) 若a=![]() ,求函數f(x)的值域.
,求函數f(x)的值域.
(2) 當f(x)在區間![]() 上為增函數時,求a的取值范圍.
上為增函數時,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一批A產品需要原材料500噸,每噸原材料可創造利潤12萬元.該公司通過設備升級,生產這批A產品所需原材料減少了x噸,且每噸原材料創造的利潤提高0.5x%;若將少用的x噸原材料全部用于生產公司新開發的B產品,每噸原材料創造的利潤為12(a﹣ ![]() x)萬元(a>0).
x)萬元(a>0).
(1)若設備升級后生產這批A產品的利潤不低于原來生產該批A產品的利潤,求x的取值范圍.
(2)若生產這批B產品的利潤始終不高于設備升級后生產這批A產品的利潤,求a的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)求函數![]() 的單調區間和極值.
的單調區間和極值.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(1)根據導數幾何意義得![]() ,再與
,再與![]() 聯立方程組解得
聯立方程組解得![]() ,
, ![]() (2)先函數導數,再求導函數零點,列表分析導函數符號變化規律,進而確定單調區間和極值
(2)先函數導數,再求導函數零點,列表分析導函數符號變化規律,進而確定單調區間和極值
試題解析:(1)![]() ,切線為
,切線為![]() ,即斜率
,即斜率![]() ,縱坐標
,縱坐標![]()
即![]() ,
, ![]() ,解得
,解得![]() ,
, ![]()
解析式![]()
(2)![]()
![]()
![]() ,定義域為
,定義域為![]()
得到![]() 在
在![]() 單增,在
單增,在![]() 單減,在
單減,在![]() 單增
單增
極大值![]() ,極小值
,極小值![]() .
.
【題型】解答題
【結束】
20
【題目】如圖:在四棱錐![]() 中,底面
中,底面![]() 為菱形,且
為菱形,且![]() ,
, ![]() 底面
底面![]() ,
,
![]() ,
, ![]() ,
, ![]() 是
是![]() 上點,且
上點,且![]() 平面
平面![]() .
.
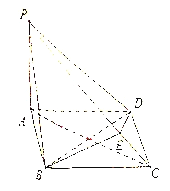
(1)求證: ![]() ;(2)求三棱錐
;(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com