
當一個非空數集 滿足條件“如果
滿足條件“如果 則
則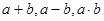
 ,并且當
,并且當 時,
時, ”時,我們就稱
”時,我們就稱 為一個數域.以下四個關于數域命題:①
為一個數域.以下四個關于數域命題:① 是任何數域的元素;②若數域
是任何數域的元素;②若數域 中有非零元素,則
中有非零元素,則 ;③集合
;③集合 是一個數域;④有理數集是一個數域.其中正確命題的序號為 .
是一個數域;④有理數集是一個數域.其中正確命題的序號為 .
①②④
解析考點:命題的真假判斷與應用.
分析:根據新定義:“如果a,b∈F,則a+b,a-b,a?b∈F,并且當b≠0時, 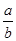 ∈F”時,我們就稱F為一個數域,對①②③④進行一一驗證,可以利用特殊值法進行判斷;
∈F”時,我們就稱F為一個數域,對①②③④進行一一驗證,可以利用特殊值法進行判斷;
解:①根據新定義a,b∈F,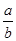 ∈F,對于a=0,可得0∈F,故①正確;
∈F,對于a=0,可得0∈F,故①正確;
②若數域F中有非零元素,F可以取實數域,可取a=2010,b=1,可得2010+1=2011∈F,故②正確;
③集合p={x|x=3k,k∈Z},p中都是3的倍數,取k=1,k=2,可得a=3,b=6,可得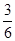 =
=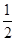 ?p,故③錯誤;
?p,故③錯誤;
④有理數是一個數域為F,對已任意a,b∈F,a+b,a-b,a?b∈F,并且當b≠0時,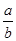 ∈F”,故④正確;
∈F”,故④正確;
故答案為:①②④;


科目:高中數學 來源: 題型:
| a | b |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年浙江省臺州市高三調研考試理數 題型:填空題
當一個非空數集 滿足條件“如果
滿足條件“如果 則
則
 ,并且當
,并且當 時,
時, ”時,我們就稱
”時,我們就稱 為一個數域.以下四個關于數域命題:①
為一個數域.以下四個關于數域命題:① 是任何數域的元素;②若數域
是任何數域的元素;②若數域 中有非零元素,則
中有非零元素,則 ;③集合
;③集合 是一個數域;④有理數集是一個數域.其中正確命題的序號為 .
是一個數域;④有理數集是一個數域.其中正確命題的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
當一個非空數集![]() 滿足條件“如果
滿足條件“如果![]() 則
則![]()
![]() ,并且當
,并且當![]() 時,
時,![]() ”時,我們就稱
”時,我們就稱![]() 為一個數域.以下四個關于數域命題:①
為一個數域.以下四個關于數域命題:①![]() 是任何數域的元素;②若數域
是任何數域的元素;②若數域![]() 中有非零元素,則
中有非零元素,則![]() ;③集合
;③集合![]() 是一個數域;④有理數集是一個數域.其中正確命題的序號為 .
是一個數域;④有理數集是一個數域.其中正確命題的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
當一個非空數集![]() 滿足條件“如果
滿足條件“如果![]() 則
則![]()
![]() ,并且當
,并且當![]() 時,
時,![]() ”時,我們就稱
”時,我們就稱![]() 為一個數域.以下四個關于數域命題:①
為一個數域.以下四個關于數域命題:①![]() 是任何數域的元素;②若數域
是任何數域的元素;②若數域![]() 中有非零元素,則
中有非零元素,則![]() ;③集合
;③集合![]() 是一個數域;④有理數集是一個數域.其中正確命題的序號為 .
是一個數域;④有理數集是一個數域.其中正確命題的序號為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com