
已知圓![]()
![]() 和點
和點![]() .
.
(1)求以點![]() 為圓心,且被
為圓心,且被![]() 軸截得的弦長為
軸截得的弦長為![]() 的圓⊙
的圓⊙![]() 的方程;
的方程;
(2)過點![]() 向圓O引切線
向圓O引切線![]() ,求直線
,求直線![]() 的方程;
的方程;
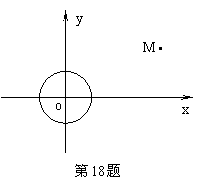 (3)設
(3)設![]() 為⊙
為⊙![]() 上任一點,過點
上任一點,過點![]() 向圓O引切線,切點為Q. 試探究:平面內是否存在一定點
向圓O引切線,切點為Q. 試探究:平面內是否存在一定點![]() ,使得
,使得![]() 為定值?若存在,請舉出一例,并指出相應的定值;若不存在,請說明理由.
為定值?若存在,請舉出一例,并指出相應的定值;若不存在,請說明理由.
解:(Ⅰ)設圓的半徑為![]() ,則
,則![]() ……………………………………3分
……………………………………3分
∴⊙![]() 的方程為
的方程為![]() ……………………………………………………5分
……………………………………………………5分
(Ⅱ)設切線![]() 方程為
方程為![]() ,易得
,易得![]() ,解得
,解得![]() ……………8分
……………8分
∴切線![]() 方程為
方程為![]() ………………………………………………………10分
………………………………………………………10分
(Ⅲ)假設存在這樣的點![]() ,點
,點![]() 的坐標為
的坐標為![]() ,相應的定值為
,相應的定值為![]() ,
,
根據題意可得![]() ,∴
,∴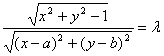 …………………………12分
…………………………12分
即![]() (*),
(*),
又點![]() 在圓上∴
在圓上∴![]() ,即
,即![]() ,代入(*)式得:
,代入(*)式得:
![]() ………………………………14分
………………………………14分
若系數對應相等,則等式恒成立,∴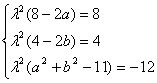 ,
,
解得![]() ,
,
∴可以找到這樣的定點![]() ,使得
,使得![]() 為定值. 如點
為定值. 如點![]() 的坐標為
的坐標為![]() 時,比值為
時,比值為![]() ;
;
點![]() 的坐標為
的坐標為![]() 時,比值為
時,比值為![]() …………………………………………………………16分
…………………………………………………………16分


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源:2012-2013學年浙江省溫州市龍灣中學高二第一次月考理科數學試卷(帶解析) 題型:解答題
已知圓 及點
及點 .
.
(1)若 為圓
為圓 上任一點,求
上任一點,求 的最大值和最小值;
的最大值和最小值;
(2)已知點 ,直線
,直線 與圓C交于點A、B.當
與圓C交于點A、B.當 為何值時
為何值時 取到最小值。
取到最小值。
查看答案和解析>>
科目:高中數學 來源:2015屆湖南省張家界市高一下學期期末聯考數學試卷A(解析版) 題型:解答題
已知圓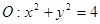 和點
和點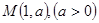 (1)若過點
(1)若過點 有且只有一條直線與圓
有且只有一條直線與圓 相切,求正實數
相切,求正實數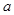 的值,并求出切線方程;(2)若
的值,并求出切線方程;(2)若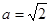 ,過點
,過點 的圓的兩條弦
的圓的兩條弦 互相垂直,設
互相垂直,設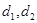 分別為圓心到弦
分別為圓心到弦 的距離.
的距離.
(Ⅰ)求 的值;
的值;
(Ⅱ)求兩弦長之積 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源:2013屆湖北省武漢市高二上學期期中數學試卷(解析版) 題型:解答題
(本題14分)已知圓 和點
和點
(1)若過點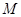 有且只有一條直線與圓
有且只有一條直線與圓 相切,求實數
相切,求實數 的值,并求出切線方程;
的值,并求出切線方程;
(2)若 ,過點
,過點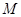 作圓的兩條弦
作圓的兩條弦 ,且
,且 互相垂直,求
互相垂直,求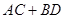 的最大值。
的最大值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com