
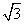 ,BD=CD=1,另一個側面是正三角形。
,BD=CD=1,另一個側面是正三角形。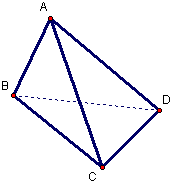
| 解:(1)作AH⊥面BCD于H,連DH AB⊥BD 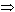 HB⊥BD, HB⊥BD,又AD=  ,BD=1 ,BD=1∴AB=  =BC=AC =BC=AC∴BD⊥DC 又BD=CD,則BHCD是正方形, 則DH⊥BC ∴AD⊥BC。 |
|
| (2)作BM⊥AC于M,作MN⊥AC交AD于N,則∠BMN就是二面角B-AC-D的平面角, 因為AB=AC=BC= 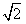 ∴M是AC的中點,且MN∥CD 則BM= 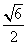 ,MN= ,MN=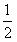 CD= CD=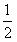 ,BN= ,BN= AD= AD=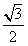 , ,由余弦定理可求得cos∠BMN= 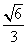 ∴∠BMN=arccos 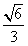 。 。(3)設E是所求的點,作EF⊥CH于F,連FD 則EF∥AH, ∴EF⊥面BCD,∠EDF就是ED與面BCD所成的角, 則∠EDF=30° 設EF=x,易得AH=HC=1,則CF=x,FD= 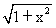 , ,∴tan∠EDF=  = =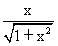 = =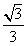 解得x= 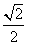 ,則CE= ,則CE=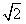 ,x=1 ,x=1故線段AC上存在E點,且CE=1時,ED與面BCD成30°角。 |
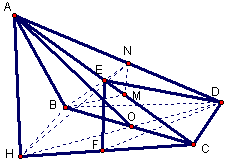 |


科目:高中數學 來源: 題型:
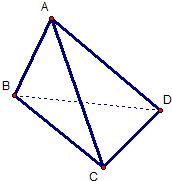 如圖,在三棱錐A-BCD中,側面ABD、ACD是全等的直角三角形,AD是公共的斜邊,且AD=
如圖,在三棱錐A-BCD中,側面ABD、ACD是全等的直角三角形,AD是公共的斜邊,且AD=| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
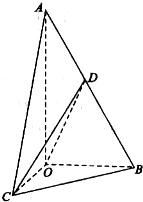 如圖,在三棱錐A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2
如圖,在三棱錐A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在三棱錐A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,點E在BC上,且AE⊥AC.
如圖,在三棱錐A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,點E在BC上,且AE⊥AC.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在三棱錐A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,∠OAB=
如圖,在三棱錐A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,∠OAB=| π | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
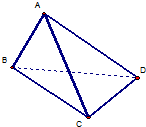 如圖,在三棱錐A-BCD中,側面ABD、ACD是全等的直角三角形,AD是公共的斜邊,且AD=
如圖,在三棱錐A-BCD中,側面ABD、ACD是全等的直角三角形,AD是公共的斜邊,且AD=| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com