
【題目】某工廠抽取了一臺設備![]() 在一段時間內生產的一批產品,測量一項質量指標值,繪制了如圖所示的頻率分布直方圖.
在一段時間內生產的一批產品,測量一項質量指標值,繪制了如圖所示的頻率分布直方圖.

(1)計算該樣本的平均值![]() ,方差
,方差![]() ;(同一組中的數據用該組區間的中點值作代表)
;(同一組中的數據用該組區間的中點值作代表)
(2)根據長期生產經驗,可以認為這臺設備在正常狀態下生產的產品的質量指標值服從正態分布![]() ,其中
,其中![]() 近似為樣本平均值,
近似為樣本平均值,![]() 近似為樣本方差
近似為樣本方差![]() .任取一個產品,記其質量指標值為
.任取一個產品,記其質量指標值為![]() .若
.若![]() ,則認為該產品為一等品;
,則認為該產品為一等品;![]() ,則認為該產品為二等品;若
,則認為該產品為二等品;若![]() ,則認為該產品為不合格品.已知設備
,則認為該產品為不合格品.已知設備![]() 正常狀態下每天生產這種產品1000個.
正常狀態下每天生產這種產品1000個.
(i)用樣本估計總體,問該工廠一天生產的產品中不合格品是否超過![]() ?
?
(ii)某公司向該工廠推出以舊換新活動,補足50萬元即可用設備![]() 換得生產相同產品的改進設備
換得生產相同產品的改進設備![]() .經測試,設備
.經測試,設備![]() 正常狀態下每天生產產品1200個,生產的產品為一等品的概率是
正常狀態下每天生產產品1200個,生產的產品為一等品的概率是![]() ,二等品的概率是
,二等品的概率是![]() ,不合格品的概率是
,不合格品的概率是![]() .若工廠生產一個一等品可獲得利潤50元,生產一個二等品可獲得利潤30元,生產一個不合格品虧損40元,試為工廠做出決策,是否需要換購設備
.若工廠生產一個一等品可獲得利潤50元,生產一個二等品可獲得利潤30元,生產一個不合格品虧損40元,試為工廠做出決策,是否需要換購設備![]() ?
?
參考數據:①![]() ;②
;②![]() ;③
;③![]() ,
,![]() .
.
【答案】(1) ![]() ;
;![]() (2) (i)見解析(ii)見解析
(2) (i)見解析(ii)見解析
【解析】
(1)根據頻率分布直方圖,用各組區間的中點值作代表可求得樣本的平均值![]() ,方差
,方差![]() 。
。
(2)根據(1)中求得的平均值![]() ,方差
,方差![]() ,可求得在
,可求得在![]() 范圍內的頻率,進而可判斷出不合格品是否超過
范圍內的頻率,進而可判斷出不合格品是否超過![]() ;或利用正太分布曲線,求
;或利用正太分布曲線,求![]() 后進行判斷。
后進行判斷。
跟題意,求得A設備與B設備的盈利均值,并根據每天多盈利額判斷即可。
(1)由頻率分布直方圖可得
![]()
![]()
![]() .
.
(2)(i)方法一:由(1)得![]() ,
,
由圖可得質量指標值在![]() 和
和![]() 的頻率為
的頻率為![]() ,
,
所以該工廠一天生產的產品中不合格品超過![]() .
.
方法二:由于![]()
![]() .
.
所以該工廠一天生產的產品中不合格品超過![]() .
.
(ii)設![]() ,
,![]() 分別為設備
分別為設備![]() ,
,![]() 一天為工廠創造的利潤,
一天為工廠創造的利潤,
則![]()
![]() ,
,
![]()
![]() ,
,
所以采用新設備利潤每天增加![]() ,
,
因此,只需56天使用設備![]() 產生的利潤就超過使用設備
產生的利潤就超過使用設備![]() 產生的利潤和換購費用總和,從長遠來看,應該換購設備
產生的利潤和換購費用總和,從長遠來看,應該換購設備![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】拋物線M:![]() 的焦點為F,過焦點F的直線l(與x軸不垂直)交拋物線M于點A,B,A關于x軸的對稱點為
的焦點為F,過焦點F的直線l(與x軸不垂直)交拋物線M于點A,B,A關于x軸的對稱點為![]() .
.
(1)求證:直線![]() 過定點,并求出這個定點;
過定點,并求出這個定點;
(2)若![]() 的垂直平分線交拋物線于C,D,四邊形
的垂直平分線交拋物線于C,D,四邊形![]() 外接圓圓心N的橫坐標為19,求直線AB和圓N的方程.
外接圓圓心N的橫坐標為19,求直線AB和圓N的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2021年福建省高考實行“![]() ”模式.“
”模式.“![]() ”模式是指:“3”為全國統考科目語文、數學、外語,所有學生必考;“1”為首選科目,考生須在高中學業水平考試的物理、歷史科目中選擇1科;“2”為再選科目,考生可在化學、生物、政治、地理4個科目中選擇2科,共計6個考試科目.
”模式是指:“3”為全國統考科目語文、數學、外語,所有學生必考;“1”為首選科目,考生須在高中學業水平考試的物理、歷史科目中選擇1科;“2”為再選科目,考生可在化學、生物、政治、地理4個科目中選擇2科,共計6個考試科目.
(1)若學生甲在“1”中選物理,在“2”中任選2科,求學生甲選化學和生物的概率;
(2)若學生乙在“1”中任選1科,在“2”中任選2科,求學生乙不選政治但選生物的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右頂點為
的左、右頂點為![]() ,
,![]() ,橢圓上任意一點
,橢圓上任意一點![]() ,滿足
,滿足![]() ,且橢圓過點
,且橢圓過點![]() .
.
(1)求橢圓的標準方程;
(2)設![]() 是軌跡
是軌跡![]() 上的兩個動點,線段
上的兩個動點,線段![]() 的中點
的中點![]() 在直線
在直線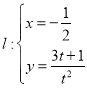 (為參數)上,線段
(為參數)上,線段![]() 的中垂線與
的中垂線與![]() 交于
交于![]() 兩點,是否存在點
兩點,是否存在點![]() ,使以
,使以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,若存在,求出
,若存在,求出![]() 點坐標,若不存在,請說明理由.
點坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的坐標為
的坐標為![]() ,若點
,若點![]() 是曲線
是曲線![]() 截直線
截直線![]() 所得線段的中點,求
所得線段的中點,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有限數列![]() 同時滿足下列兩個條件:
同時滿足下列兩個條件:
①對于任意的![]() (
(![]() ),
),![]() ;
;
②對于任意的![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() 三個數中至少有一個數是數列
三個數中至少有一個數是數列![]() 中的項.[來
中的項.[來
(1)若![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)證明:![]() 不可能是數列
不可能是數列![]() 中的項;
中的項;
(3)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com