
已知函數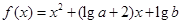 滿足
滿足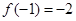 , 且對于任意
, 且對于任意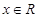 恒有
恒有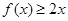 成立。
成立。
(1) 求實數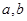 的值;
的值;
(2)設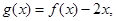 若存在實數
若存在實數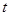 ,當
,當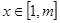 時,
時,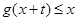 恒成立,求實數
恒成立,求實數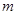 的最大值。
的最大值。
(1)b=10, a=100;(2) 實數 的最大值是4。
的最大值是4。
【解析】(1)由f(-1)=-2,代入函數解析式得到關于lga與lgb的等式記作①,化簡后得到關于a與b的等式記作②,又因為f(x)≥2x恒成立,把f(x)的解析式代入后,令△≤0得到關于lga與lgb的不等式,把①代入后得到關于lgb的不等式,根據平方大于等于0,即可求出b的值,把b的值代入②即可求出a的值;
(1)由f(-1)=-2知,lgb-lga+1=0①,所以a b =10②.又f(x)≥2x恒成立,f(x)-2x≥0恒成立,則有x2+x•lga+lgb≥0恒成立,故△=(lga)2-4lgb≤0,將①式代入上式得:(lgb)2-2lgb+1≤0,即(lgb-1)2≤0,故lgb=1即b=10,代入②得,a=100;
(2) 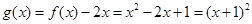 ,∵存在實數
,∵存在實數 ,當
,當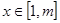 時,
時, 恒成立;即
恒成立;即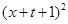
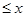 恒成立.
恒成立.
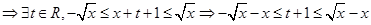 (
(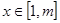 )恒成立.
)恒成立.
設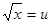 ,則
,則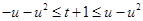
∴ ,即
,即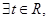
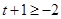 ,且
,且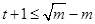
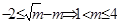 ,∴實數
,∴實數 的最大值是4。
的最大值是4。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
已知函數![]() 滿足
滿足![]() ,且
,且![]()
(1)當![]() 時,求
時,求![]() 的表達式;
的表達式;
(2)設![]() ,
,![]() ,求證:
,求證:![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
(3)設![]() ,對每一個
,對每一個![]() ,在
,在![]() 與
與![]() 之間插入
之間插入![]() 個
個![]() ,得到新數列
,得到新數列![]() ,設
,設![]() 是數列
是數列![]() 的前
的前![]() 項和,試問是否存在正整數
項和,試問是否存在正整數![]() ,使
,使![]() ?若存在求出
?若存在求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省高三5月模擬考試文科數學試卷(解析版) 題型:選擇題
已知函數 滿足
滿足 ,且
,且 ,若對任意的
,若對任意的 ,
,
總有 成立,則
成立,則 在
在 內的可能值有( )個.
內的可能值有( )個.
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中數學 來源:2011年廣東省高二第一次階段性測試題文科數學 題型:解答題
(本小題滿分14分)已知函數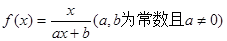 滿足
滿足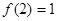 ,且
,且 有唯一實數解。
有唯一實數解。
(1)求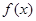 的表達式 ;
的表達式 ;
(2)記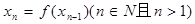 ,且
,且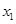 =
=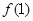 ,求數列
,求數列 的通項公式。
的通項公式。
(3)記 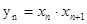 ,數列{
,數列{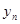 }的前
}的前 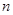 項和為
項和為
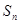 ,是否存在k∈N*,使得
,是否存在k∈N*,使得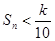 對任意n∈N*恒成立?若存在,求出k的最小值,若不存在,請說明理由.
對任意n∈N*恒成立?若存在,求出k的最小值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2013屆度廣東省高二理科數學月考試卷 題型:解答題
已知函數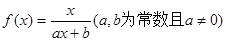 滿足
滿足 ,且
,且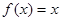 有唯
有唯
一實數解。
(1)求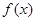 的表達式 ;
的表達式 ;
(2)記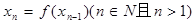 ,且
,且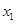 =
=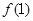 ,求數列
,求數列 的通項公式。
的通項公式。
(3)記 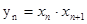 ,數列{
,數列{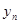 }的前
}的前 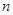 項和為
項和為
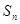 ,是否存在k∈N*,使得
,是否存在k∈N*,使得
對任意n∈N*恒成立?若存在,求出k的最小值,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com