
已知函數f(x)=x+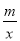 ,且f(1)=2.
,且f(1)=2.
(1)求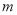 ;
;
(2)判斷 的奇偶性;
的奇偶性;
(3)函數 在
在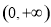 上是增函數還是減函數?并證明.
上是增函數還是減函數?并證明.
(1)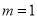 ;(2)奇函數;(3)增函數.
;(2)奇函數;(3)增函數.
【解析】
試題分析:(1)根據題意將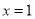 帶入
帶入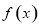 的解析式中,得到關于
的解析式中,得到關于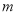 的方程,進而求得
的方程,進而求得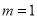 的值;(2)根據(1)得到
的值;(2)根據(1)得到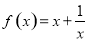 ,再根據函數奇偶性的定義判斷其奇偶性,首先確定定義域關于原點對稱,其次判斷
,再根據函數奇偶性的定義判斷其奇偶性,首先確定定義域關于原點對稱,其次判斷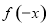 與
與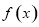 的關系,得到
的關系,得到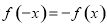 ,則原函數為奇函數;(3)根據函數單調性的定義,首先在
,則原函數為奇函數;(3)根據函數單調性的定義,首先在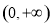 任取
任取 且
且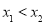 ,帶入函數
,帶入函數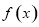 中,用作差法比較
中,用作差法比較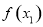 與
與 的大小,得到
的大小,得到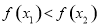 所以原函數在
所以原函數在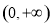 上為增函數.
上為增函數.
試題解析:(1)f(1)=1+m=2,m=1. 2分
(2)f(x)=x+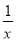 ,f(-x)=-x-
,f(-x)=-x-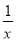 =-f(x),∴f(x)是奇函數. 6分
=-f(x),∴f(x)是奇函數. 6分
(3)設x1、x2是(1,+∞)上的任意兩個實數,且x1<x2,則 7分
f(x1)-f(x2)=x1+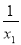 -(x2+
-(x2+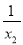 )=x1-x2+(
)=x1-x2+(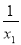 -
-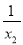 )
)
=x1-x2-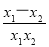 =(x1-x2)
=(x1-x2)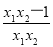 . 10分
. 10分
當1<x1<x2時,x1x2>1,x1x2-1>0,從而f(x1)-f(x2)<0,
即f(x1)<f(x2).
∴函數f(x)=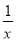 +x在(1,+∞)上為增函數. 12分
+x在(1,+∞)上為增函數. 12分
考點:1.函數解析式;2.函數奇偶性;3.函數單調性.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源:[同步]2014年蘇教版必修三 3.4互斥事件練習卷(解析版) 題型:?????
一袋中有紅、黃、藍三種顏色的小球各一個,每次從中取出一個,記下顏色后放回,當三種顏色的球全部取出時停止取球,則恰好取5次球時停止取球的概率為( )
A.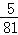 B.
B.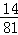 C.
C.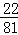 D.
D.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年重慶市高一上學期第三次定時練習數學試卷(解析版) 題型:選擇題
已知[x]表示不超過實數x的最大整數, 為取整函數,
為取整函數, 是方程
是方程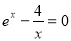 的根 (e為自然對數的底數),則
的根 (e為自然對數的底數),則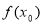 等于 ( )
等于 ( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中數學 來源:2014-2015學年云南德宏州芒市高一上學期期末考試數學試卷(解析版) 題型:選擇題
設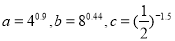 ,則 ( )
,則 ( )
A.c>a>b B.b>a>c C.a>b>c D.a>c>b
查看答案和解析>>
科目:高中數學 來源:2014-2015學年江西省贛州市北校高二1月月考文科數學試卷(解析版) 題型:填空題
設拋物線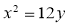 的焦點為
的焦點為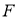 ,經過點
,經過點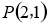 的直線
的直線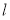 與拋物線相交于
與拋物線相交于 兩點且點
兩點且點 恰為
恰為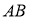 的中點,則
的中點,則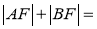 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com