分析:(Ⅰ)當E為AB的中點時,ME∥平面ADD1A1.取DD1的中點N,連接MN、AN、ME,證明 ME∥AN,即可證明ME∥平面AD1.
(Ⅱ)當E為AB的中點時,結合二面角A-D1E-C的大小為二面角A-D1E-D與二面角D-D1E-C大小的和,只需求二面角A-D1E-D的大小即可;過A點作AF⊥DE交DE于F,過F作FH⊥D1E于H,連接AH,則∠AHF即為二面角A-D1E-D的平面角,通過AH•D1E=AE•AD1然后求出sin∠AHF,即可求出二面角A-D1E-C的大小.
解答:
證明:(Ⅰ)當E為AB的中點時,ME∥平面ADD
1A
1.
證明:取DD
1的中點N,連接MN、AN、ME,
MN∥
CD,AE∥
CD,
∴四邊形MNAE為平行四邊形,可知 ME∥AN
∵AN在平面AD
1內
∴ME∥平面AD
1.
(Ⅱ)當E為AB的中點時,DE=
,CE=
,又CD=2,
可知∠DEC=90°,所以DE⊥CE,平面CED
1⊥平面DD
1E,
所以二面角D-D
1E-C的大小為
;
又二面角A-D
1E-C的大小為二面角A-D
1E-D與二面角D-D
1E-C大小的和,
只需求二面角A-D
1E-D的大小即可;
過A點作AF⊥DE交DE于F,則AF⊥平面DD
1E,AF=
,
過F作FH⊥D
1E于H,連接AH,
則∠AHF即為二面角A-D
1E-D的平面角,
在Rt△AED
1中,又AH•D
1E=AE•AD
1,
∴AH=
=
=
=
,
∴sin∠AHF=
=
=
,
所以二面角A-D
1E-C的大小為
+arcsin.
點評:本題考查直線與平面平行,二面角的求法,考查轉化思想,空間想象能力,計算能力.

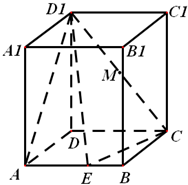 在長方體ABCD-A1B1C1D1中,AD=1,AA1=AB=2,點E是AB中點,點M為D1C的中點.
在長方體ABCD-A1B1C1D1中,AD=1,AA1=AB=2,點E是AB中點,點M為D1C的中點. 證明:(Ⅰ)當E為AB的中點時,ME∥平面ADD1A1.
證明:(Ⅰ)當E為AB的中點時,ME∥平面ADD1A1.

 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案 (2013•上海) 如圖,在長方體ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.證明直線BC′平行于平面D′AC,并求直線BC′到平面D′AC的距離.
(2013•上海) 如圖,在長方體ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.證明直線BC′平行于平面D′AC,并求直線BC′到平面D′AC的距離. (2009•青浦區二模)(理)在長方體ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦區二模)(理)在長方體ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在長方體ABCD-A′B′C′D′中,點E為棱CC′上任意一點,AB=BC=2,CC′=1.
已知在長方體ABCD-A′B′C′D′中,點E為棱CC′上任意一點,AB=BC=2,CC′=1.