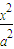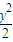日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
已知雙曲線-=1（a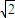＞）的兩條漸近線的夾角為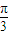，則雙曲線的離心率為（ ）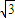
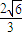
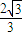
A．2
B．
C．
D．
【答案】分析：雙曲線（a＞）的漸近線方程是，由題設條件可知，從而求出a的值，進而求出雙曲線的離心率．
解答：解：∵雙曲線（a＞）的漸近線方程是
∴由雙曲線（a＞）的兩條漸近線的夾角為可知，
∴a2=6，c2=8，∴雙曲線的離心率為，故選D．
點評：本題考查雙曲線的性質及其應用，解題的關鍵是由漸近線的夾角求出a．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

已知雙曲線=1（a＞0，b＞0）的右焦點為F，右準線與一條漸近線交于點A，△OAF的面積為 (O為原點)，則兩條漸近線的夾角為（    ）

A.30°             B.45°              C.60°              D.90°

查看答案和解析>>

科目：高中數學 來源：2012-2013學年山西省晉中市昔陽中學高二（上）第二次月考數學試卷（理科）（解析版） 題型：解答題

已知雙曲線=1（a＞0，b＞0）的離心率為，右準線方程為．
（Ⅰ）求雙曲線C的方程；
（Ⅱ）已知直線x-y+m=0與雙曲線C交于不同的兩點A，B，且線段AB的中點在圓x2+y2=5上，求m的值．

查看答案和解析>>

科目：高中數學 來源：2012-2013學年安徽省六安市壽縣迎河中學高二（上）第三次月考數學試卷（理科）（解析版） 題型：解答題

已知雙曲線=1（a＞0，b＞0）的離心率為，右準線方程為．
（Ⅰ）求雙曲線C的方程；
（Ⅱ）已知直線x-y+m=0與雙曲線C交于不同的兩點A，B，且線段AB的中點在圓x2+y2=5上，求m的值．

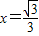查看答案和解析>>

科目：高中數學 來源：2011-2012學年江蘇省南通市啟東市匯龍中學高二（上）第二次學情調查數學試卷（解析版） 題型：解答題

已知雙曲線=1（a＞0，b＞0）的離心率為，右準線方程為．
（Ⅰ）求雙曲線C的方程；
（Ⅱ）已知直線x-y+m=0與雙曲線C交于不同的兩點A，B，且線段AB的中點在圓x2+y2=5上，求m的值．

查看答案和解析>>

科目：高中數學 來源：2010-2011學年貴州省冊亨縣民族中學高三（上）期末數學試卷（文科）（解析版） 題型：解答題

已知雙曲線=1（a＞0，b＞0）的離心率為，右準線方程為．
（Ⅰ）求雙曲線C的方程；
（Ⅱ）已知直線x-y+m=0與雙曲線C交于不同的兩點A，B，且線段AB的中點在圓x2+y2=5上，求m的值．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 国产精品免费一区二区 | 三级黄网站 | 亚洲精品一区二区三区蜜桃久 | www.超碰在线 | 亚洲黄色三级 | 久久久天堂 | 嗯嗯嗯亚洲精品国产精品一区 | 国产18av| 国产精品日韩精品 | 欧美精品一区二区三区在线 | 另类免费视频 | 日本另类αv欧美另类aⅴ | 欧美视频在线一区 | 伊人在线 | 中国91视频 | 国产精品一区二区免费视频 | 久久久久久九九九九 | 18毛片 | 日韩国产精品一区二区三区 | 欧美另类一区二区 | 国产高清免费视频 | 亚洲一区久久 | 久久精品国产免费 | 国产精品视频一区二区免费不卡 | 亚洲一区二区三区免费在线观看 | 亚洲成人精品av | 一区二区久久 | 国产精品1区二区 | 久久久久久亚洲精品中文字幕 | 日韩中文字幕免费在线播放 | 久久久99精品免费观看 | 亚洲日本欧美日韩高观看 | 涩涩av | 欧美精品网 | h在线观看 | 91一区二区 | 日日综合 | 亚州国产精品 | 一级女性全黄久久生活片免费 | 一区二区日韩 | 欧美日韩免费一区 |