
【題目】已知函數![]() .
.
(1)當![]() 時,求證:對
時,求證:對![]() 時,
時, ![]() ;
;
(2)當![]() 時,討論函數
時,討論函數![]() 零點的個數.
零點的個數.
【答案】(1)見解析;(2)見解析.
【解析】試題分析:(1)函數求導![]() ,再求導得
,再求導得![]() 恒成立,又因為
恒成立,又因為![]() 恒成立;
恒成立;
(2)由(1)可知,當x≤0時,f″(x)≤0,可得 對x∈R,f′(x)≥0,即ex≥x+1,分類討論當x≥-1時,當x<-1時,函數y=f(x)的零點個數即可得解;
當x<-1時,再分0≤m≤1和m<0兩種情況進行討論,由函數零點定理進行判斷即可得到答案.
試題解析:,所以
(1)當![]() 時,
時, ![]() ,則
,則![]() ,令
,令![]() ,則
,則![]() ,當
,當![]() 時,
時, ![]() ,即
,即![]() ,所以函數
,所以函數![]() 在
在![]() 上為增函數,即當
上為增函數,即當![]() 時,
時, ![]() ,所以當
,所以當![]() 時,
時, ![]() 恒成立,所以函數
恒成立,所以函數![]() 在
在![]() 上為增函數,又因為
上為增函數,又因為![]() ,所以當
,所以當![]() 時,對
時,對![]() 恒成立.
恒成立.
(2)由(1)知,當![]() 時,
時, ![]() ,所以
,所以![]() ,所以函數
,所以函數![]() 的減區間為
的減區間為![]() ,增函數為
,增函數為![]() .所以
.所以![]() ,所以對
,所以對![]()
![]() ,
, ![]() ,即
,即![]() .
.
①當![]() 時,
時, ![]() ,又
,又![]() ,
, ![]() ,即
,即![]() ,所以當
,所以當![]() 時,函數
時,函數![]() 為增函數,又
為增函數,又![]() ,所以當
,所以當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,所以函數
,所以函數![]() 在區間
在區間![]() 上有且僅有一個零點,且為
上有且僅有一個零點,且為![]() .
.
②當![]() 時,(ⅰ)當
時,(ⅰ)當![]() 時,
時, ![]() ,所以
,所以![]() ,所以函數
,所以函數![]() 在
在![]() 上遞增,所以
上遞增,所以![]() ,且
,且![]() ,故
,故![]() 時,函數
時,函數![]() 在區間
在區間![]() 上無零點.
上無零點.
(ⅱ)當![]() 時,
時, ![]() ,令
,令![]() ,則
,則![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增,
上單調遞增, ![]() ,當
,當![]() 時,
時, 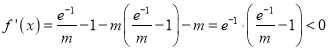 ,又曲線
,又曲線![]() 在區間
在區間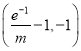 上不間斷,所以
上不間斷,所以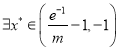 ,使
,使![]() ,故當
,故當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,所以函數
,所以函數![]() 的減區間為
的減區間為![]() ,增區間為
,增區間為![]() ,又
,又![]() ,所以對
,所以對![]() ,又當
,又當![]() 時,
時, ![]() ,又
,又![]() ,曲線
,曲線![]() 在區間
在區間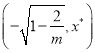 上不間斷.所以
上不間斷.所以![]() ,且唯一實數
,且唯一實數![]() ,使得
,使得![]() ,綜上,當
,綜上,當![]() 時,函數
時,函數![]() 有且僅有一個零點;當
有且僅有一個零點;當![]() 時,函數
時,函數![]() 有個兩零點.
有個兩零點.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】在參加市里主辦的科技知識競賽的學生中隨機選取了40名學生的成績作為樣本,這40名學生的成績全部在40分至100分之間,現將成績按如下方式分成6組:第一組,成績大于等于40分且小于50分;第二組,成績大于等于50分且小于60分;……第六組,成績大于等于90分且小于等于100分,據此繪制了如圖所示的頻率分布直方圖.在選取的40名學生中.

(1)求成績在區間![]() 內的學生人數及成績在區間
內的學生人數及成績在區間![]() 內平均成績;
內平均成績;
(2)從成績大于等于80分的學生中隨機選3名學生,求至少有1名學生成績在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x2﹣4x+a,g(x)=logax(a>0且a≠1).
(1)若函數f(x)在[﹣1,3m]上不具有單調性,求實數m的取值范圍;
(2)若f(1)=g(1)
①求實數a的值;
②設t1= ![]() f(x),t2=g(x),t3=2x , 當x∈(0,1)時,試比較t1 , t2 , t3的大小.
f(x),t2=g(x),t3=2x , 當x∈(0,1)時,試比較t1 , t2 , t3的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前項和為Sn , 且a2=2,S5=15,數列{bn}的前項和為Tn , 且b1= ![]() ,2nbn+1=(n+1)bn(n∈N*)
,2nbn+1=(n+1)bn(n∈N*)
(Ⅰ)求數列{an}通項公式an及前項和Sn;
(Ⅱ) 求數列{bn}通項公式bn及前項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司制定了一個激勵銷售人員的獎勵方案:當銷售利潤不超過8萬元時,按銷售利潤的15%進行獎勵;當銷售利潤超過8萬元時,若超出A萬元,則超出部分按log5(2A+1)進行獎勵.記獎金為y(單位:萬元),銷售利潤為x(單位:萬元).
(1)寫出獎金y關于銷售利潤x的關系式;
(2)如果業務員小江獲得3.2萬元的獎金,那么他的銷售利潤是多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC的內角A,B,C所對的邊分別為a,b,c,若bcosC+ccosB=asinA,則△ABC的形狀為( )
A.銳角三角形
B.直角三角形
C.鈍角三角形
D.不確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2x﹣8,g(x)=2x2﹣5x﹣18
(1)求不等式g(x)<0的解集
(2)若對一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知命題p:方程 ![]() 表示焦點在y軸的橢圓;命題q:關于x的不等式x2﹣2x+m>0的解集是R; 若“p∧q”是假命題,“p∨q”是真命題,求實數m的取值范圍.
表示焦點在y軸的橢圓;命題q:關于x的不等式x2﹣2x+m>0的解集是R; 若“p∧q”是假命題,“p∨q”是真命題,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(Ⅲ)若這100名學生語文成績某些分數段的人數(![]() )與數學成績相應分數段的人數(
)與數學成績相應分數段的人數(![]() )之比如表所示,求數學成績在
)之比如表所示,求數學成績在![]() 之外的人數.
之外的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com