
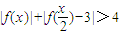 ;
;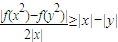 .
.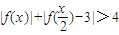 ,根據絕對值不等式的代數意義去絕對值符號,轉化為解一元一次不等式;把求得的結果求并集;(II)把函數f(x)=2x+1代入
,根據絕對值不等式的代數意義去絕對值符號,轉化為解一元一次不等式;把求得的結果求并集;(II)把函數f(x)=2x+1代入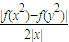 ,根據絕對值的運算性質放縮不等式,即可證得結論.
,根據絕對值的運算性質放縮不等式,即可證得結論. 時,不等式化為-2x-1+2-x>4,
時,不等式化為-2x-1+2-x>4, <x<2時,不等式化為2x+1+2-x>4,
<x<2時,不等式化為2x+1+2-x>4, ,此時x≥2.
,此時x≥2.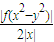 =
=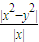 =
= =
=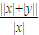 •||x|-|y||=|1+
•||x|-|y||=|1+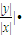 ||x|-|y||,
||x|-|y||,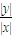 |≥1,當y=0時取等號,
|≥1,當y=0時取等號,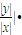 ||x|-|y||≥||x|-|y||≥|x|-|y|
||x|-|y||≥||x|-|y||≥|x|-|y|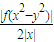 ≥|x|-|y|.
≥|x|-|y|.

 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案科目:高中數學 來源: 題型:
| 1 |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com