
【題目】在直角坐標(biāo)系中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為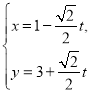 (
(![]() 為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸,建立極坐標(biāo)系,曲線
軸正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出![]() 的普通方程及
的普通方程及![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點(diǎn)![]() 在
在![]() 上,點(diǎn)
上,點(diǎn)![]() 在
在![]() 上,求
上,求![]() 的最小值及此時點(diǎn)
的最小值及此時點(diǎn)![]() 的直角坐標(biāo).
的直角坐標(biāo).
【答案】(1)![]() ,
,![]() .(2)
.(2) ![]() ,
,![]() .
.
【解析】
(1)由曲線![]() 的參數(shù)方程消去
的參數(shù)方程消去![]() ,即可得到直線的普通方程,根據(jù)極坐標(biāo)與直角坐標(biāo)的互化公式,即可求得曲線
,即可得到直線的普通方程,根據(jù)極坐標(biāo)與直角坐標(biāo)的互化公式,即可求得曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)![]() 的參數(shù)方程為
的參數(shù)方程為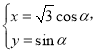 (
(![]() 為參數(shù)),得到
為參數(shù)),得到![]() ,結(jié)合點(diǎn)到直線的距離公式和三角函數(shù)的性質(zhì),即可求解.
,結(jié)合點(diǎn)到直線的距離公式和三角函數(shù)的性質(zhì),即可求解.
(1)由曲線![]() 的參數(shù)方程
的參數(shù)方程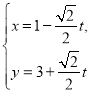 (
(![]() 為參數(shù)),消去
為參數(shù)),消去![]() ,可得
,可得![]() ,
,
由![]() ,即
,即![]() ,
,
又由![]() ,
,![]() 代入方程,可得
代入方程,可得![]() ,
,
即曲線![]() 的直角坐標(biāo)方程
的直角坐標(biāo)方程![]() .
.
(2)設(shè)![]() 的參數(shù)方程為
的參數(shù)方程為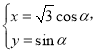 (
(![]() 為參數(shù)),
為參數(shù)),![]() ,則
,則![]() .
.
因為![]() 是直線,所以
是直線,所以![]() 的最小值即為
的最小值即為![]() 到
到![]() 距離
距離![]() 的最小值,
的最小值,
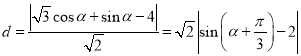 ,
,
當(dāng)![]() 時,
時,![]() 取得最小值
取得最小值![]() , 此時
, 此時![]() 為
為![]() .
.


 作業(yè)輔導(dǎo)系列答案
作業(yè)輔導(dǎo)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
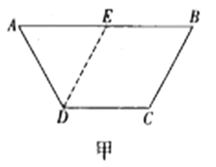
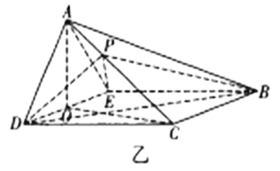
【題目】如圖甲,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn).將
的中點(diǎn).將![]() 沿
沿![]() 折起,使二面角
折起,使二面角![]() 為
為![]() ,連接
,連接![]() ,
,![]() 得到四棱錐
得到四棱錐![]() (如圖乙),
(如圖乙),![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 是棱
是棱![]() 上一點(diǎn).
上一點(diǎn).
(1)求證:當(dāng)![]() 為
為![]() 的中點(diǎn)時,平面
的中點(diǎn)時,平面![]() 平面
平面![]() ;
;
(2)是否存在一點(diǎn)![]() ,使平面
,使平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() ,若存在,求
,若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知在直角坐標(biāo)系xOy中,圓C的參數(shù)方程為![]() (θ為參數(shù)),直線l經(jīng)過定點(diǎn)P(2,3),傾斜角為
(θ為參數(shù)),直線l經(jīng)過定點(diǎn)P(2,3),傾斜角為![]() .
.
(Ⅰ)寫出直線l的參數(shù)方程和圓C的標(biāo)準(zhǔn)方程;
(Ⅱ)設(shè)直線l與圓C相交于A,B兩點(diǎn),求|PA|·|PB|的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】圖①中△ABC 為直角三角形![]() D、E 分別為 AB、AC 的中點(diǎn),將△ADE 沿 DE 折起使平面 ADE⊥BCED,連接 AB,AC,BE如圖②所示.
D、E 分別為 AB、AC 的中點(diǎn),將△ADE 沿 DE 折起使平面 ADE⊥BCED,連接 AB,AC,BE如圖②所示.
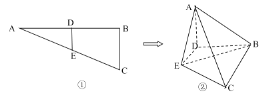
(1)在線段AC上找一點(diǎn)P,使EP∥平面ABD,并求出異面直線AB、EP所成的角;
(2)在平面ABD內(nèi)找一點(diǎn)Q,使PQ⊥平面ABE,并求三棱錐P-ABE的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知多面體![]() 的底面
的底面![]() 是邊長為2的菱形,
是邊長為2的菱形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() .
.
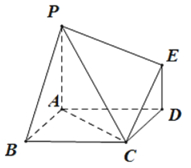
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成的角為45°,求平面
所成的角為45°,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)當(dāng)![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)![]() 時,令
時,令![]() ,是否存在區(qū)間
,是否存在區(qū)間![]() ,使得函數(shù)
,使得函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的值域為
上的值域為![]() ,若存在,求實數(shù)
,若存在,求實數(shù)![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】鳳梨穗龍眼原產(chǎn)廈門,是廈門市的名果,栽培歷史已有100多年.龍眼干的級別按直徑![]() 的大小分為四個等級(如下表).
的大小分為四個等級(如下表).
|
|
|
|
|
級別 | 三級品 | 二級品 | 一級品 | 特級品 |
某商家為了解某農(nóng)場一批龍眼干的質(zhì)量情況,隨機(jī)抽取了100個龍眼干作為樣本(直徑分布在區(qū)間![]() ),統(tǒng)計得到這些龍眼干的直徑的頻數(shù)分布表如下:
),統(tǒng)計得到這些龍眼干的直徑的頻數(shù)分布表如下:
|
|
|
|
|
|
頻數(shù) | 1 |
| 29 |
| 7 |
用分層抽樣的方法從樣本的一級品和特級品中抽取6個,其中一級品有2個.
(1)求![]() 、
、![]() 的值,并估計這批龍眼干中特級品的比例;
的值,并估計這批龍眼干中特級品的比例;
(2)已知樣本中的100個龍眼干約500克,該農(nóng)場有500千克龍眼干待出售,商家提出兩種收購方案:
方案![]() :以60元/千克收購;
:以60元/千克收購;
方案![]() :以級別分裝收購,每袋100個,特級品40元/袋、一級品30元/袋、二級品20元/袋、三級品10元/袋.
:以級別分裝收購,每袋100個,特級品40元/袋、一級品30元/袋、二級品20元/袋、三級品10元/袋.
用樣本的頻率分布估計總體分布,哪個方案農(nóng)場的收益更高?并說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com